VNITŘNÍ ZTRÁTY LOPATKOVÝCH STROJŮ A JEJICH VLIV NA NÁVRH LOPATKOVÉHO STROJE

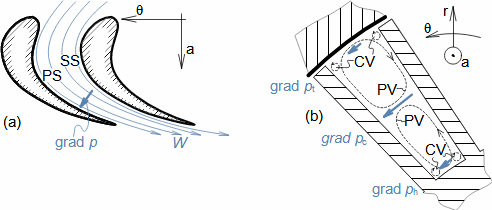
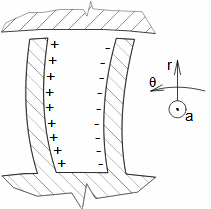
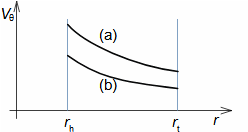
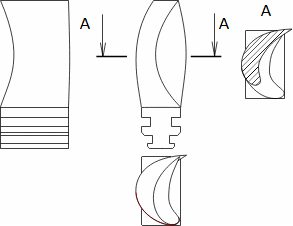
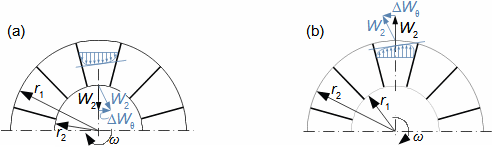
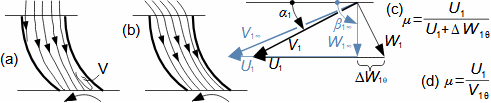
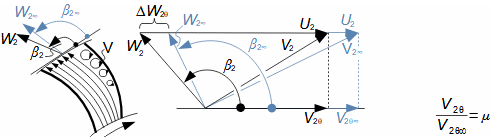
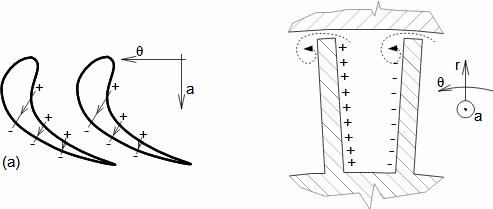
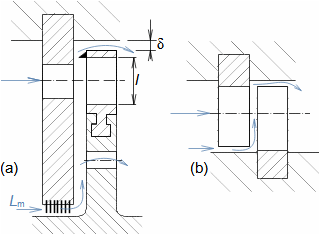
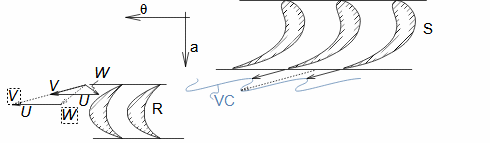
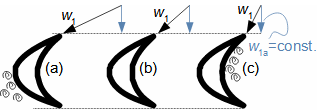
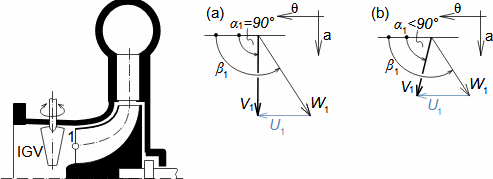
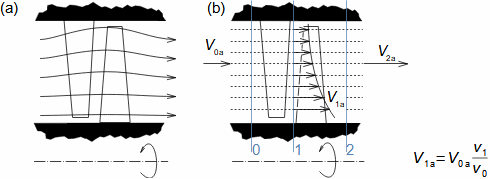
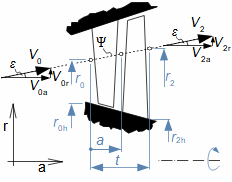
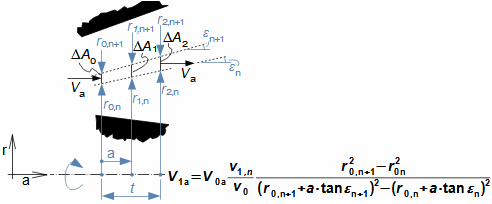
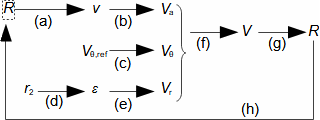
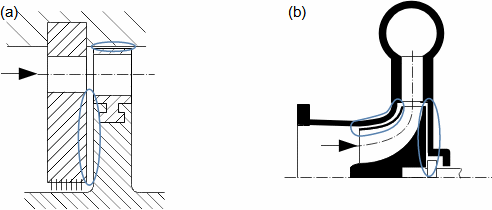
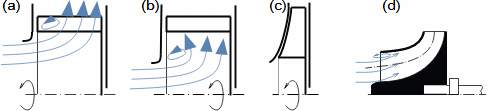
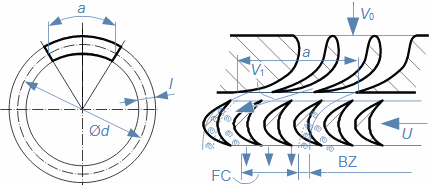
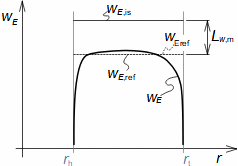
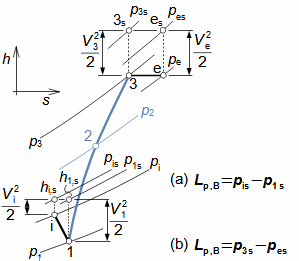
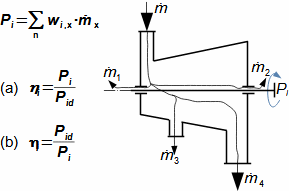
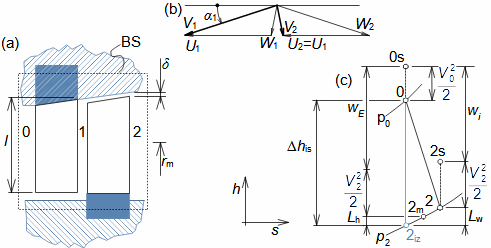
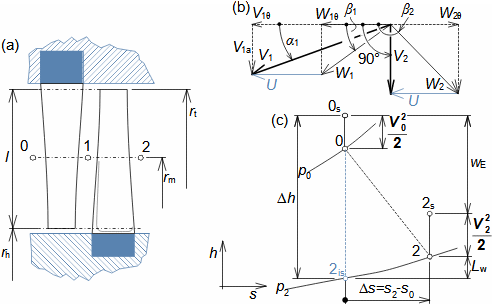
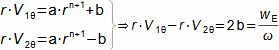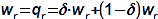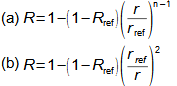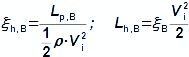Základní pojmy pro popis vnitřních ztrát v lopatkových strojích

Vnitřní ztráty L_w jako rozdíl mezi ideální práci a skutečnou prací stroje vznikají vždy při nějaké transformaci nebo přenosu energie v různých částech stroje s různou intenzitou. Kromě profilových ztrát vznikají i další typy vnitřních ztrát, například netěstnostmi, třením pracovní tekutiny o skříň a hřídel apod. Jednotlivé typy ztrát jsou definovány tak, aby se při výsledné energetické bilanci stroje daly sečíst a tím získat konečnou velikost vnitřních ztrát podle Vzorce 1. Nicméně mnoho typů ztrát se navzájem více či méně ovlivňují a při konečném vyčíslení je nutné toto brát v úvahu. Výpočet vnitřních ztrát se provádí v rámci jednoho stupně (vnitřní ztráty stupně) nebo celého stroje vnitřní ztráty stroje apod.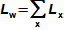

1: Vnitřní ztráty

L_w [J·kg^-1] vnitřní ztráty ve vyšetřované části stroje; L_x [J·kg^-1] hodnota individuální ztráty ve vyšetřované části stroje. x-označení vyšetřovaného druhu ztráty.

Poměrná ztráta

Podíl individuální ztráty k ideální práci (disponibilní energie) je poměrná ztráta (Vzorec 2a), ovšem podle typu stroje, ztrát a zvyklostí v daném oboru ji lze definovat i k vnitřní práci (Vzorec 2b) nebo jinému ději.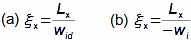

2: Poměrná ztráta

ξ_x [1] poměrná ztráta individuální ztráty; w_id [J·kg^-1] ideální práce pracovní tekutiny; w_i [J·kg^-1] vnitřní práce pracovní tekutiny.

Výpočet ztrát

Ideální děj

Výpočet ztrát je podmíněn znalostí rozměrů a parametrů vyšetřované části stroje a definicí ideálního děje (stavu). To znamená, že stanovení ztrát probíhá iteračně. Například tak, že na počátku se provede návrh stroje nebo jeho části pro případ proudění beze ztrát, nebo pouze s odhady ztrát, a až po tomto návrhu se vypočítají skutečných ztráty a provedou případné změny v rozměrech a parametrech za účelem snížení ztrát atd. Při výpočtu se vychází nejčastěji z polo-empirických vztahů vyvinutých pro daný typ stroje, numerických výpočtů (modelování) nebo ze schopnosti konstruktéra využít širokých znalostí chování podobných strojů/stupňů k predikci ztráty pro nový doposud neřešený případ.

Nátokový úhel

Machovo číslo

Dixon and Hall, 2010

Velikost ztráty sekundárním prouděním roste například se zvětšujícím se nátokovým úhlem a s klesajícím Machovým číslem. Predikce změn úhlů rychlostí vlivem sekundárního proudění u zkroucených lopatek je provedena například v [Dixon and Hall, 2010, s. 212].

Prohnutá lopatka

Nakloněná lopatka

Japikse, 1997

Ke zmenšení ztráty sekundárním proudění axiálních stupň se provádí naklonění lopatek od radiální osy, ale účinější je jejich prohnutí (Obrázek 4) [Japikse, 1997, s. 6-13].

4: Prohnutá lopatka

Prohnutá lopatka

Axiální stupeň

Eulerova práce

Tvar prohnuté lopatky axiálního stupně se nenavrhuje za podmínky konstantní cirkulace obvodové složky rychlosti (podmínka potenicálního víru), ale naopak za podmínky její změny podle nějaké exponeciální funkce. Například podle funkce definované Rovnicí 5, viz Obrázek 6. Tato rovnice je výhodná v tom, že Eulerova práce po výšce lopatek je konstantní jako u potenciálního proudění (rovnice potenciálního víru je speciálním případem této rovnice).

5: Rovnice axiálního stupně s konstantní Eulerovou prací a exponenciální cirkulací rychlosti

V [m·s^-1] absolutní rychlost; r [m] poloměr; w_E [J·kg^-1] Eulerova práce na vyšetřovaném poloměru; ω [rad·s^-1] úhlová rychlost otáčení rotoru; a, n [SI] navržené konstanty; b [SI] konstanta (lze vypočítat z navržené Eulerovy práce na referenčním poloměru).

8: Protiběžný vír v lopatkovém kanálu radiálního stupně

(a) směr protiběžného víru; (b) dostředivé proudění; (c) odstředivé proudění. Ω [rad·s^-1] úhlová rychlost protiběžného víru; a_r [m·s^-2] odstředivé zrychlení; a_c [m·s^-2] Coriolisovo zrychlení.

Radiální složka rychlosti

Obvodová složka rychlosti

Skluz

Přímým důsledkem působení víru je nerovnoměrné rozložení radiální složky rychlosti proudění v lopatkovém kanálu (na jedné straně ji urychluje, ale na druhé straně kanálu ji zpomaluje) a změna obvodové složky výtokové rychlosti, které se říká skluz (Obrázek 9(a, b)). Protiběžný vír ve výsledku snižuje hodnotu Eulerovy práce kvůli nevýhodné změně obvodové složky rychlosti W_2θ a tedy i V_2θ na výtoku z rotoru.

9: Změna radiálních a obvodových složek rychlosti v důsledku působení protiběžného víru

ΔW_θ [m·s^-1] odchylka obvodové složky relativní rychlosti na výtoku z rotoru, kterou způsobyl protiběžný vír.

Součinitel skluzu

Dixon and Hall, 2010

K predikci vlivu protiběžného víru na Eulerovu práci se používá veličina nazývaná součinitel skluzu. Skluz je definován zvlášť u stupňů turbín (Obrázek 10) a zvlášť u stupňu pracovních strojů (Obrázek 11).

10: Definice součinitele skluzu radiální cetripetální turbíny

(a) vliv protiběžného víru na proudění; (b) v případě centripetálních turbín je možné kompenzovat skluz změnou úhlu absolutní rychlosti před rotorem, tím se změní i úhel relativní rychlosti; (c) obecný vzorec pro součinitel skluzu; (d) speciální vzorec pro součinitel skluzu při β_1∞=90° (vzorce pro jiné případy, například [Dixon and Hall, 2010, s. 279]). μ [1] součinitel skluzu pro centripetální turbíny; β [°] úhel relativní rychlosti. V-víry, které vznikají při odtržení proudu od lopatek. Index _∞ označuje parametry rychlostního trojúhelníku pro případ nekonečného počtu lopatek (případ, kdy nevzniká protiběžný vír).

13: Ztráty vnitřní netěsností

(a) nětěsnost u rovnotlakového stupně s diskovým rotorem a lopatkami s bandážemi; (b) ztráta vnitřní netěsností u stupně bez bandáží. L_m [kg·s^-1] hmotnostní tok netěstnostmi stupně; δ [m] délka radiální mezery; l [m] délka lopatky.

Diskový rotor

Japikse, 1997

Zekui, 2025

Proudění netěsnostmi může narušit hlavní proud, protože má vyšší energii. V případě diskových rotorů, se proto netěsnost předchozí řady lopatek odsává otvorem v disku mimo lopatkové kanály (Obrázek 13a). Netěsnost lopatek bez bandáže obvlivňuje i okrajovou ztrátu, viz Úloha 1. Vztahy pro přibližné stanovení ztráty vnitřní netěsností jsou uvedeny v [Japikse, 1997, s. 6-35], [Zekui et. al., 2025] (v češtině [Kadrnožka, 2004, s. 95, 200]).

Misárek, 1963

Poměrná ztráta vnitřní netěsností klesá s délkou lopatek, respektive s poměrem délky lopatek l a radiální mezery δ. U stupňů pracovních strojů se navíc může v některých provozních stavech projevit netěsnost kladně, protože stabilizuje proudění stupně. Závislost délky lopatek na účinnost stupně kompresoru je uvedena například v [Misárek, 1963, s. 73].

Ztráta nerovnoměrností rychlostního pole před mříží

Mezní vrstva

Rychlostní trojúhelník

Na výstupu z lopatkové mříže je nerovnoměrné rychlostní pole, které je způsobeno třením v mezní vrstvě proudu u ploch lopatek na sací i přetlakové straně. Toto nerovnoměrné rozložení rychlosti pracovní tekutiny způsobuje, že při pohybu rotorové řady lopatek, která prochází takovým rychlostním polem, se střídavě mění nátokový úhel i rychlost, respektive rychlostní trojúhelník, viz Obrázek 14.

Natáčivé lopatky

Otáčky

Předřazené lopatky

Optimální nátokový úhel při změně průtoku stupněm lze zachovat změnou otáček. Jestli není možné otáčky měnit, pak lze nátokový úhel udržovat v optimálních mezí natáčením lopatek. U jednostupňových axiálních a radiálních pracovních strojů lze také použít natáčivé předřazené lopatky, viz Obrázek 16. Při změně průtoku se předřazené statorové lopatky natočí tak, aby se co nejméně měnil vstupní uhel relativní rychlosti do mříže rotoru, tím se dosáhne co nejmenšího poklesu účinnosti kvůli změně nátkového úhlu.

16: Regulace nátokového úhlu do rotoru radiálního stupně kompresoru pomocí předřazených statorových lopatek

(a) rychlostní trojúhleník na nátokové hraně záběrníku v připadě jmenovitého průtoku; (b) odklon absolutní rychlosti od osového směru pomocí předřazených lopatek, tak aby vstupní úhel β₁ zůstal zachován i při sníženém průtoku. IGV-předřazené statorové lopatky (inlet guide vane). α [°] úhel absolutní rychlosti; β [°] úhel relativní rychlosti rychlosti.

Ztráta zpětným prouděním

Tento typ ztráty souvisí se snížením hmotnostním tokem stupně oproti jmenovitému stavu. V případě sníženého průtoku může dojít k významnému odtržení proudu od omezujících meridiálních ploch lopatkových kanálů (u pat lopatek) a zpětnému proudění, jak ukazuje Obrázek 17. To je způsobeno působením odstředivých sil na pracovní tekutinu.

17: Zpětné proudění u dlouhé zkroucené lopatky při zmenšení průtoku stupněm turbíny

Ztráty změnou meridánové rychlosti

Výtoková rychlost

Průtočný průřez

Je snahou, aby výtoková rychlost lopatkového stroje byla stejná jako vtoková. Jestliže je vyšší, pak mluvíme o ztrátě v kinetické energii výtokové rychlosti, což je energie pracovní tekutiny, která se netrasformovala na vnitřní práci stroje – místo toho se zvýšila kinetická energie pracovní tekutiny. Samozřejmě jsou případy, kdy je zvýšení výtokové rychlosti žádoucí (vrtule, proudové motory apod.). Změna meridánové rychlosti může generovat i další typy ztrát. Například u tepelných turbín během expanze dochází ke zvyšování měrného objemu a při stejných průtočných průřezech se zvyšuje nejen výtoková rychlost, ale i profilové ztráty. Obdobně je to při kompresi v turbokompresorech, kde při stejných průtočných průřez dochází k poklesu rychlosti. To znamená, že může klesnout ztráta třením, ale s poklesem rychlosti je nutné zvětšit prohnutí lopatek (pro zachování stejné Eulerovy práce stupně, respektive obvodové složky rychlosti), což může vést k odtržení proudu od lopatek.

Normální stupeň

Zkroucené lopatky

U tepelných turbín a turbokompresorů je tedy nutné postupně průtočné průřezy měnit tak, aby vtoková a výtoková rychlost stupně zůstavály přibližně stejné. Stupně s touto podmínkou se také nazývají normální stupně. Zatím co u radiálních stupňů změny průtočných průřezů na vtoku a výtoku nemají podstaný vliv na postup návrhu stupně, tak u axiálních stupňů je zásah do návrhu mnohem významnější, protože je nutné uvažovat i o radiální složce rychlosti, tak jak se mění délky lopatek – proto už hovoříme o kuželovém stupni, viz Obrázek 19.

19: Příklady provedení kuželových stupňů se zkroucenými lopatkami

ε [°] úhel mezi axiálním směrem a směrem po kuželové ploše. Další příklady kuželových stupňů jsou uvedeny článku Termodynamika tepelných turbín.

Stupeň reakce

Stupeň reakce R pro jednotlivé poloměry se musí počítat iteračně. Nejprve se provede odhad stupně reakce pro vyšetřovaný poloměr a z něj se stanoví parametry pracovního plynu, ze kterých se následně spočítají rychlosti a stupeň reakce jehož hodnota se porovná s odhadem, viz Obrázek 22.

22: Iterační výpočet stupně reakce axiálního stupně

R [1] stupeň reakce. (a) odhad stupně reakce R a z h-s diagramu nebo výpočtem určit měrný objem na výtoku z první řady lopatek; (b) výpočet axiální složky rychlosti; (c) výpočet obvodové složky rychlosti ze vzorce pro konstantní cirkulaci rychlosti a zadaného trojúhelníku na referenčním poloměru; (d) výpočet výtokového poloměru stupně podle Vzorce 20 a úhlu ε; (e) výpočet radiální složky rychlosti; (f) výpočet absolutní rychlosti; (g) výpočet stupně reakce z rychlostí; (h) porovnání s původním odhadem stupně reakce, jestliže přesnost odhadu nebyla dostatečná, pak se výpočet opakuje s novým odhadem. Index _ref označuje zadané parametry na referenčním poloměru.

Kadrnožka, 2004

Pfleiderer and Petermann, 2005

Výše uvedený postup návrhu kuželového stupně je pouze jeden z mnoha možných variant, například v [Kadrnožka, 2004], [Pfleiderer and Petermann, 2005] se sklon kuželových ploch předepisuje a následně iteračně dopočítává vtoková a výtoková rychlost stupně na jednotlivých poloměrech.

Ventilační ztráta rotoru

Rotor

Eulerova práce

Tření

Diskový rotor

Radiální stupeň

Bandáž

Ventilační ztráta rotoru je ekvivalentní části Eulerovy práce, kterou je třeba vynaložit k překonání třecího odporu pracovní tekutiny proti otáčení rotoru – takže průměrná hodnota Eulerovy práce musí být větší než vnitřní práce stupně. Významná ventilační ztráta vzniká například u diskových konstrukcí rotoru (Obrázek 23a), kde je relativně velká plocha disku ve styku s pracovní tekutinou uzavřenou mezi diskem a statorem. Dále je významná u radiálních stupňů (Obrázek 23b). Ventilační ztráta také vzniká na vymezujících plochách mezi rotorem a statorem (bandáží), ale tato ztráta bývá relativně malá.

Misárek, 1963

Rozsáhlé informace z měření vlivu jednotlivých typů ztrát na účinnost radiálního kompresorového stupně jsou uvedeny v [Misárek, 1963].

Ztráta parciálním ostřikem

Odtržení proudu

Tření

Kadrnožka, 2004

Ztráta parciálním ostřikem vzniká v případech, kdy tekutina vtéká do stupně pouze na části obvodu rotorové řady lopatek, viz Obrázek 26. Samotná ztráta je realizována v okrajových pásmech (víření tekutiny v důsledku odtrhávání proudu od lopatek) a třením lopatek o "statickou" pracovní tekutinu mimo pracovní oblast. Podrobnosti k mechanismu vzniku ztráty parciálním ostřikem a její přibližný výpočet je v [Kadrnožka, 2004, s. 196].

26: Parciálního ostřik rotorové řady lopatek

a [m] délka statorové řady lopatek (skupiny trysek); l [m] délka lopatek; FC-jádro proudu (flow core); BZ-okrajové pásmo (border zone).

Lavalova turbína

Skupinová regulace

Spalovací turbíny

Ztráta parciálním ostřikem se vyskytuje u jednostupňových turbín např. Lavalových turbín (kde statorová řada lopatek nebývá po celém obvodu) nebo u skupinové regulace parních turbín a také u spalovacích turbín s trubkovými spalovacími komorami.

Příklad postupu při návrhu stupně se ztrátami

Model

Při rozhodávání o postupu návrhu stupně lopatkového stroje se berou v úvahu požadavky na jeho výkonové parametry, cenu, náklady na provoz, způsob provozu i podle toho zda se jedná o stroj pro sériovou výrobu nebo kusovou. Z toho důvodu nelze popsat univerzální postup výpočtu ztrát lopatkového stroje. O návrhu průtočných částí lopatkových strojů lze obecně říci, že je lze navrhnout podle analytických výpočtových modelů a optimalizovat a zpřesnit jejich parametry pomocí počítačových výpočtových modelů.

28: Stupeň reakce axiálního stupně s konstantní Eulerovou prací a nestlačitelnou tekutinu

(a) stupeň reakce pro případ návrhu obvodové složky rychlosti podle Vzorce 5; (b) stupeň reakce pro případ návrhu obvodové složky rychlosti podle rovnice pro potenciální vír (n=-1). Index _ref označuje veličinu na referenčním poloměru lopatky. Odvození je uvedeno v Příloze 5.

Ztráty v hrdlech lopatkových strojů

Hrdla musí udržovat rovnoměrný tlak tekutiny na celém obvodu vtokové části prvního a výtokové části posledního stupně stroje. Ve vtokových hrdlech je pracovní tekutina obvykle mírně urychlována směrem k prvnímu stupni. Ve výtokových hrdlech je pracovní tekutina obvykle mírně zpomalována směrem od posledního stupně. V obou případech se změnou rychlostí kompenzuje tlaková ztráta. Ztráta v hrdlech je obvykle vztažena ke kinetické energii tekutiny před hrdlem, viz Vzorec 29.

29: Poměrná a měrná ztráta v hrdle

L_h,B [J·kg^-1] ztráta v hrdle; V_i [m·s^-1] střední rychlost ve vtokovém průřezu hrdla; L_p [Pa] tlaková ztráta v hrdle; ρ [kg·m^-3] hustota; ξ_B [1] poměrná ztráta hrdla.

h-s diagram hrdla

Na Obrázku 30 je h-s diagram termodynamických změn probíhajících v hrdlech pracovního stroje. Tlak ve vtokovém hrdle se postupně snižuje tak, jak se snižuje průtočný průřez (probíhá zde sání). Ve výtokovém hrdle probíhá přibližně škrcení, aby byla kompenzována tlaková ztráta hrdla (klesá celkový tlak), případně zde probíhá mírná komprese pro stabilizaci mezní vrstvy. Zejména u ventilátorů náslduje za výtokovým hrdlem ještě přímý difuzor, ve kterém se část kinetické energie plynu transformuje na tlakovou energii.

Úlohy

(a) meridiální řez stupněm; (b) rychlostní trojúhleník na středním poloměru; (c) h-s diagram stupně. η_E [1] účinnost Eulerovy práce; l [mm] délka lopatek; α [°] úhel absolutní rychlosti; W [m·s^-1] relativní rychlost; h [J·kg^-1] entalpie; s [J·kg^-1·K^-1] entropie; L_h [kJ·kg^-1] profilové ztráty na středním poloměru; L_w [kJ·kg^-1] vnitřní ztráty; Δh_is [kJ·kg^-1] izoentropický rozdíl entalpií; m [kg·s^-1] hmotnostní tok. Index _m označuje střední poloměr lopatek.