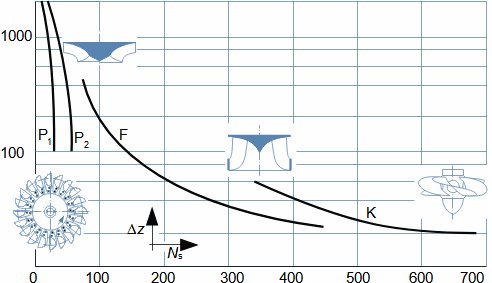
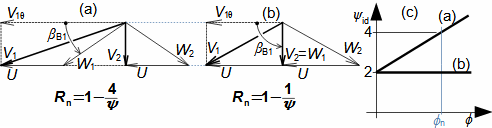
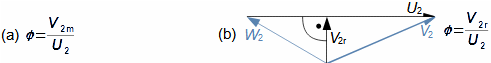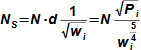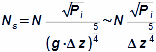Lopatkový strojKinematická podobnostVšechny lopatkové stroje jsou si podobné svým principem, který lopatkové stroje odlišuje od ostatních. Nejčastěji se snažíme nalézt podobnosti, respektive podobnostní součinitelé mezi dvěma lopatkovými stroji, jestliže jejich pracovní tekutiny mají podobné vlastnosti, mají podobnou geometrii a kinematiku pohybu pracovní tekutiny (tzv. kinematická podobnost). Takové podobnostní součinitele si konstruktéři mohou sestavit za určitých okolností sami (pokud mají k dispozici velké množství naměřených dat z modelů či předchozích strojů), ale obvyklejší je vycházet z již zavedených podobnostních součinitelů, které sestavili generace lidí, kteří si všimli, většinou na základě dlouhodobého pozorování a prací na strojích, že poměry některých parametrů jsou u jednotlivých typů strojů stejné při optimálních parametrech. V následujích částech článku jsou uvedeny nejčastěji používané podobnostní součinitele v oboru lopatkových strojů. Geometrická podobnost stupňů lopatkových strojůLopatková mřížRadiální ventilátorJedná se o vyhledávání podobnosti v geometrii zejména lopatkových mříží a tím i tvaru rychlostních trojúhelníků. Mezi základní geometrické podobnosti patří typ stroje podle meridánového směru proudění a geometrické charakteristiky lopatkové mříže jako je hustota lopatkové mříže apod., viz Obrázek 1. 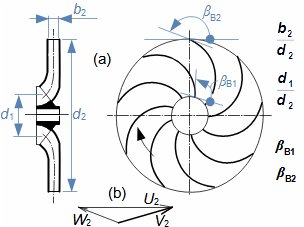 1: Typické geometrické podobnostní součinitelé rotoru radiálního ventilátoru Z tvaru/typu rotoru (a) lze určit tvar rychlostního trojúhelníku (b). b [m] šířka; βB [°] úhly profilu; d [m] průměr; U [m·s-1] obvodová rychlost; W [m·s-1] relativní rychlost pracovní tekutiny; V2 [m·s-1] absolutní rychlost pracovní tekutiny. Index 1 označuje vstup do oběžného kola, index 2 výstup. |