TVARY LOPATEK A PRŮTOČNÝCH ČÁSTÍ LOPATKOVÝCH STROJŮ

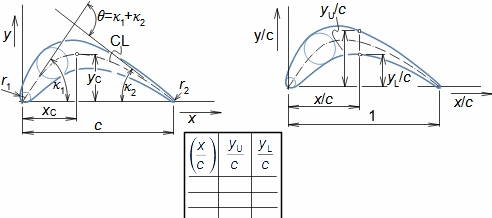
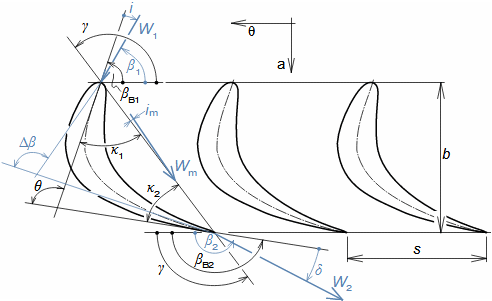
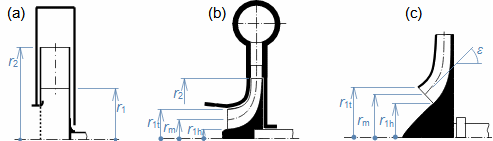
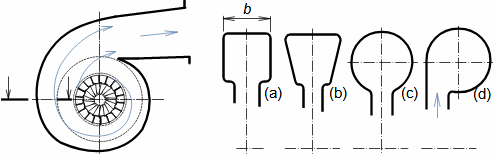
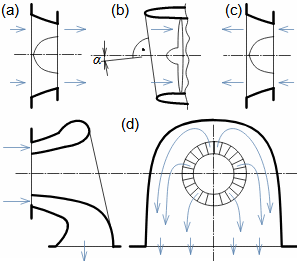
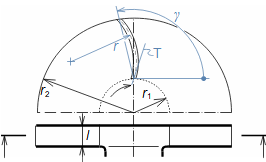
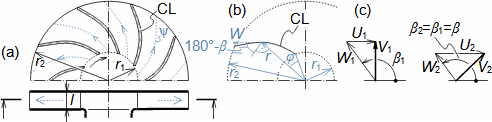
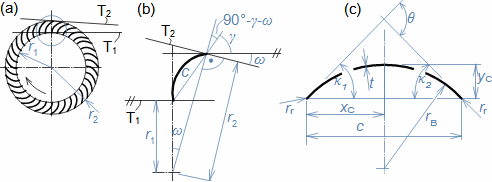
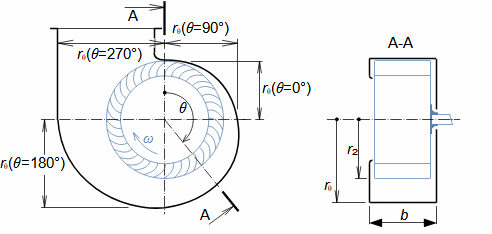
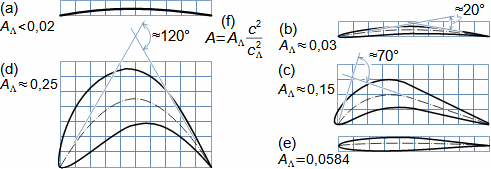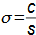Typy profilových mříží

Úhel nastavení profilu

Konfuzorová mříž

Rovnotlaková mříž

Difuzorová mříž

Typ profilové mříže je dán úhlem nastavení profilu (natočením v mříži). Zásádní pro výsledné rychlosti pracovní tekutiny při průtoku profilovou mříží je velikost vstupního a výstupního průřezu mříže. Přičemž ze stejného profilu lze sestavit jakýkoliv základní typ profilové mříže se stejnou roztečí pouze natočením profilu, respektive změnou úhlu nastavení profilu v mříži, viz Obrázek 1: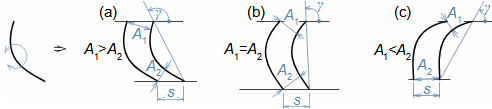

1: Vztahy mezi základními typy profilových mříží

(a) konfuzorová mříž – též názvy přetlaková, turbínová; (b) rovnotlaková mříž – při stejném průtočném průřezu se nemění tlak a rychlost mezi vstupem a výstupem; (c) difuzorová mříž – též název přetlaková, kompresorová nebo turbínová pro případ, že A₁ je kritický průřez. A [m²] průtočný průřez v daném místě mříže. γ [°] úhel nastavení profilu v mříži; s [m] rozteč. Profil jsou zjednodušeně kresleny jakoby byly vyrobeny z plechu.

Profil lopatky

Profilem lopatky je myšlen její obrys na konkrétním řezu. V rámci této kapitoly jsou popsány metody k vytvoření výkresu profilu lopatky a pravidla ke stanovení tvaru profilu lopatky.

Výkres profilu

Souřadnice profilu

Střední čára profilu

Tětiva

Zaznamenat profil lopatky lze pomocí pravidel pro geometrii profilu lopatek. Výběr způsobu zápisu tvaru profilu lopatek zavisí na nosiči tohoto zápisu, respektive se jedná o nejvhodnější způsob ve vztahu k požadované formě výrobní dokumentace. V současnosti stačí grafický výstup (pomocí vektorové grafiky), např. v CAD systémech, protože obráběcí stroje a výpočtové softwary jsou schopné s takovým výstupem pracovat přímo, ale existují i jiné formy zápisu profilu lopatky. Například se zapisují tabelárně v souřadnicích x; y a pomocí tvaru střední čáry profilu, viz Obrázek 2.

Letecké profily

Abbott and Doenhoff, 1959

Vhodný profil lze vybrat z katalogů profilů na základě aerodynamických požadavků. Tvary a aerodynamická data profilů tenkých a málo zakřivených lze odečíst z rozsáhlých katalogů profilů používaných v letectví, například [Abbott and Doenhoff, 1959]. Pokud vhodný profil lopatky v katalogu chybí, je nutné jej vyvinout a experimentálně ověřit.

Základní profil

Při vývoji nového profilu se obvykle vychází z různých prohnutí tzv. základního profilu, což je symetrický hladký profil, viz Obrázek 3. Existuje mnoho základních profilů odlišující se od sebe tvarem, aerodynamickými charakteristikami a dalšími vlastnostmi, viz například [Abbott and Doenhoff, 1959]. Vývoj nového profilu vzniklého prohnutím základního profilu umožňuje systematicky definovat aerodynamické rozdíly mezi různými prohnutími a tyto nové profily přehledně katalogizovat, podle toho z jakého základního profilu vychází.

3: Základní profil a profil vzniklý prohnutím tohoto profilu

Pevnost

Průřez profilu

Střední čára profilu

Mimo aerodynamických požadavků musí profil splňovat i pevnostní požadavky, které ovlivňují potřebnou tloušťku profilu u paty lopatek, kde je nejvyšší namáhání od odstředivých sil i od ohybu. Na Obrázku 4 jsou typické profilu u pat lopatek pro vybrané aplikace a jejich průřez.

4: Měrné průřezy profilů u pat lopatek

(a) profil běžný u radiálních stupňů a axiálních s velmi malým prohnutím; (b) tenký profil s malým zakřivením proudu běžný u hydraulických strojů či turbokompresorů (střední čára profilu kružnice); (c) profil málo zatížených lopatek tepelných turbín (střední čára profilu kružnice a přímka); (d) profil velmi zatížené lopatky tepelných turbín (střední čára profilu parabola); (e) profil lopatky větrných turbín (NACA 63-209); (f) vzorec pro přepočet průřezu profilu pro různou délku tětivy podle Cavalieriova principu. A [mm²] skutečný průřez profilu lopatky; A_Λ [mm²] průřez profilu lopatky při délce tětivy c_Λ (čísla u profilů na tomto obrázku jsou pro délku tětivy 1 mm, tzv. měrný průřez profilu).

Hustota profilové mříže

Počet lopatek

Schopnost proudu dosáhnou požadovaného zakřivení není funkcí pouze prohnutí střední čáry profilu, ale také rozteče profilové mříže, délkou tětivy, respektive počtu lopatek, přičemž poměr mezi délkou tětivy a roztečí profilové mříže je označován jako hustota profilové mříže, viz Vzorec 6.

6: Hustota profilové mříže

σ [1] hustota profilové mříže.

Difuzorové mříže

Konfuzorové mříže

Střední šířka lopatkového kanálu

Pfleiderer, 2005

Při větší hustotě profilové mříže lze očekávat větší zakřivení proudu a naopak. Na druhou stranu s hustotou profilové mříže roste počet lopatek a ztráty třením v mříži. Existuje tedy optimální hodnota hustoty profilové mříže. V případě difuzorových profilových mříží je nutno hledat jejich optimální hustotu takovou, při které bude poměr c/a_m kolem 2,5, kde a_m je střední šířka lopatkového kanálu [Pfleiderer and Petermann, 2005, s. 408], viz Vzorec 7. V případě konfuzorových mříží bývá uvedený poměr menší než 2,5. Uvedené poměry platí pro profilové mříže složené z tenkých málo zakřivených profilů.

7: Odhad optimální hustoty profilove mříže

a_m [m] střední šířka lopatkového kanálu. Odvození rovnice je provedeno v Příloze 5.

Zweifelův součinitel

Japikse, 1997

Hustotu profilové mříže s velmi prohnutými profily tepelných turbín lze přibližně stanovit podle Zweifelova součinitele. Zweifelův součinitel C_L,θ je podíl obvodové složky síly na lopatku od proudu tekutiny F_θ ku součinu plochy lopatky a dynamického tlaku relativní rychlosti na výstupu z lopatkové mříže, viz Vzorec 8. Hodnota tohoto součinitele by u navržené profilové mříže měla být v rozsahu 0,75...0,85 u moderních profilů z velkou pevností materiálu lopatek až 1 [Japikse, 1997, s. 6-17].

Radiální stupeň

Úhly střední čáry profilu

Francisova turbína

Vlastnosti radiálních stupňů podstatně závisí na úhlu střední čáry profilu na obvodu rotoru (Obrázek 9), viz bezrozměrové charakteristiky radiálních stupňů. Nicméně nejlepší aerodynamické vlastnosti mají dozadu zahnuté lopatky jejichž střední čáry profilu odpovídá logaritmické spirále, viz Úloha 1. V případě turbínových radiálních stupňů se s jiným úhelem střední čáry profilu na obvodu rotoru než s úhlem 90° lze setkat prakticky jen u Francisových turbín.

9: Vliv úhlu střední čáry profilu na tvar lopatek radiálních stupňů pracovních strojů

(a) dozadu zahnuté lopatky; (b) radiální lopatky; (c) dopředu zahnuté lopatky.

Tvary lopatek

Tvar lopatky může být jednak přímý, tj. jedná se o lopatku se stejným profilem po její délce, jednak zkroucený, u kterého se po délce lopatky tvar profilu i úhel nastavení profilu mění. Mimo tyto dva základní tvary lze ještě mluvit o tvarech lopatek radiálních stupňů.

Přímé lopatky

Přímé lopatky axiálních stupňů se obvykle používají tam, kde lze dosáhnout malý poměr mezi délkou lopatky a středním poloměrem lopatky, takže se prostorový charakter proudění tolik neprojevuje. Výhodou přímých lopatek je jednoduchý návrh, výroba, respektive náklady na výrobu. Často bývají vyráběny tažením jako dráty kruhového profilu, viz Obrázek 10.

11: Rozkrucování zkroucené lopatky

(a) znázornění směru rozkrucování zkroucené lopatky působením odstředivých sil; (b) zkroucená lopatka s integrovaným tlumičem vibrací.

Radiální lopatky

Krycí disk

Lopatky radiálních stupňů jsou buď takového tvaru, že vytváří čistě radiální lopatkové kanály, nebo takové, že zasahují i do axiálního směru (Obrázek 12(b, c)). V případě čistě radiálních lopatek se jedná většinou o přímé lopatky často konstantní šířky někdy vyrobené z plechu (viz Úloha 3).

12: Příklady provedení radiálních lopatek u pracovních strojů

(a) čistě radiální lopatky; (b), (c) radiálně-axiální lopatky (v případě (c) jsou lopatky opatřeny krycím diskem pro snížení vnitřní netěsnosti). Index _t označuje špici lopatky, _h patu lopatky či poloměr hřídele. r_m [m] střední poloměr lopatky (v tomto případě na vstupu); ε [°] sklon proudnice vůči ose rotace.

Záběrník

Kavitace

Axiální část radiálních lopatek se používá u stupňů turbín i pracovních strojů. U turbín má funkci rovnoměrného převedení proudění z radiálního do axiálního směru se snížením obvodové složky rychlosti V_2θ. Axiální část se u stupňů pracovních strojů nazývá záběrník. U čerpadel bývá záběrník nevýrazný (Obrázek 12c), aby se zabránilo velkým rozdílům mezi rychlostmi u pat a špic lopatek záběrníku, což by mohlo způsobit kavitaci. Axiální část radiálního oběžného kola se počítá na třech poloměrech, tedy mimo středního ještě na špici a u paty lopatky, tak aby nátokový úhel u pracovních strojů nebo úhel deviační u turbín byl po výšce lopatky stálý (viz 2D-výpočet záběrníku). Výroba této části lopatky obráběním je náročná a proto se takový typ rotoru skládá z více částí – viz Obrázek 13.

Spirální hrdla

Základní návrh spirálního hrdla vychází z teorie potenciálního proudění, při kterém proudnice mají tvar logaritmické spirály. Základní tvary spirálních hrdel jsou ukázány na Obrázku 14, přičemž některé tvary nesplňují podmínky rovnic pro potenciální proudění, takže v nich vznikají víry. Nicméně mají jiné výhody – zejména snižují potřebný průměr spirálního hrdla, který vychází při konstantní šířce hrdla a potenciálním proudění mnohem větší než průměr rotoru. Spirální hrdla lze zmenšit i jejich ukončením při menších stupních než při 360°, viz Úloha 4 – zkrácená hrdla lze použít tam, kde je velikost důležitější parametr než účinnost.

14: Základní tvary spirálních hrdel

(a) obdélníková (konstantní šířka hrdla – použití především u ventilátorů); (b) lichoběžníková (postupné rozšiřování vede na nižší ztráty než skokové rozšíření a jeho tvar je velmi blízký podmínce pro potenciální proudění); (c) kruhová; (d) tangenciální výstupní hrdlo. b [m] šířka hrdla.

Axiální hrdla

Boční hrdla

Turbokompresorový motor

Mattingly et al., 2002

Na Obrázku 15 jsou některá provedení axiálních a bočních hrdel. V případě Obrázku 15b se jedná o šikmo seříznuté axiální hrdlo turbokompresorového motoru, které umožňuje optimálnější rozložení tlaku před prvním stupněm turbokompresoru. Maximální výkon motoru (spotřeba vzduchu) je při vzletu letounu, a proto úhel α přibližně odpovídá úhlu stoupání během startu. Více o této problematice, včetně výpočtu optimálního odklonu α je uvedeno v [Mattingly et al., 2002, s. 424].

15: Hrdla axiálních stupňů

(a) axiální vstupní hrdlo (například vstupní hrdlo spalovací turbíny); (b) vstupní hrdlo turbokompresorového motoru; (c) axiální výstupní hrdlo (například výstupní hrdlo axiálního ventilátoru); (d) boční hrdla (například boční hrdla axiálního kompresoru). α [°] odklon osy sání od osy motoru.

(a) rotor; (b) detail kótování nastavení profilu v mříži; (c) výrobní výkres lopatky. ω [°] pomocný úhel.

Odkazy