AERODYNAMIKA PROFILOVÝCH MŘÍŽÍ

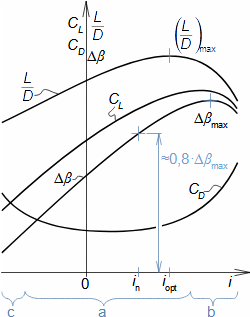
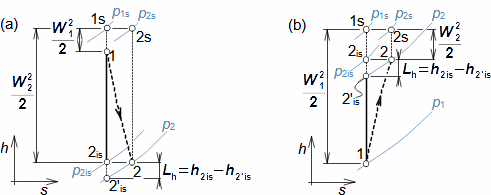
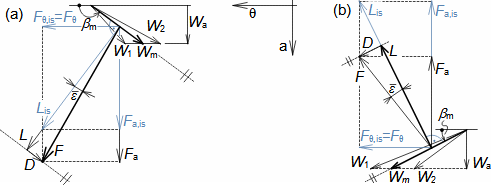
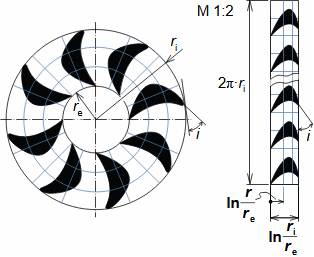
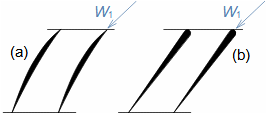
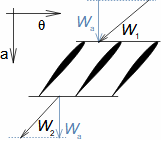
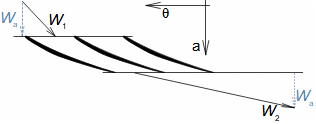
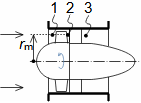
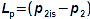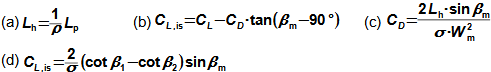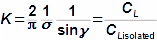Základní pojmy aerodynamiky profilových mříží

Aerodynamika leteckých profilů

Odpor

Vztlak

Aerodynamika profilové mříže vychází z definic aerodynamických veličin používáných při popisu aerodynamiky leteckých profilů [Škorpík, 2022, Aerodynamika profilů]. To znamená, že u profilu zařazeného do profilové mříže lze také rozlišovat odpor a vztlak, které lze vypočítat podle stejných vzorců jako v případě osamocených profilů, s tím rozdílem, že místo nátokové rychlosti se vychází ze střední aerodynamické rychlosti v mříži, takže odpor je ve směru této střední rychlosti a vztlak kolmý na tuto rychlost, viz Vzorce 1.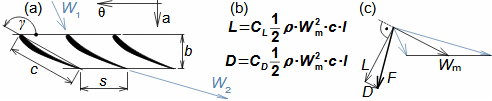

1: Vzorce pro odpor a vztlak lopatky v lopatkové mříži

(b) řez rovinnou lopatkovou mříží; (b) vzorce pro výpočet odporu a vztlaku přímé lopatky v rovinné lopatkové mříži; (c) vztahy mezi rychlostmi a silami působící na přímou lopatku. D [N] odpor; L [N] vztlak; F [N] výsledná síla působící na lopatku; ρ [kg·m^-3] hustota pracovní tekutiny; W_m [m·s^-1] střední aerodynamická rychlost v mříži; c [m] tětiva profilu; γ [°] úhel nastavení profilu v mříži; b [m] šířka lopatkové mříže; l [m] délka přímé lopatky; C_D, C_L [1] součinitel odporu a vztlaku profilu v profilové mříži; s [m] rozteč. θ, a-označení os v soustavě souřadnic.

Součinitel vztlaku

Součinitel odporu

Aerodynamický tunel

Japikse,1997

Aerodynamické součinitelé C profilů v mříži jsou měřeny v aerodynamických tunelech rovinných lopatkových mříží, viz Obrázek 2 pro různou kombinaci rychlostí a nátokových úhlů. Lopatková mříž v aerodynamické tunelu je tvořena několika (5 až 7) přímými lopatkami vloženými do průtokového kanálu šikmo tak, aby proud pracovní tekutiny odpovídal směru relativní rychlosti ve skutečné lopatkové mříži. Vstupní a výstupní průřez tunelu odpovídá průtočným průřezům testované lopatkové mříže. Konstrukce aerodynamického tunelu kompresorových lopatkových mříží jsou uvedeny např. v [Japikse, 1997, s. 11-7] a pro turbínové lopatkové mříže [Japikse, 1997, s. 6-22].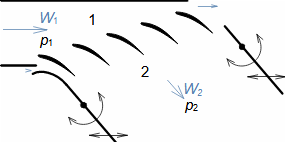

2: Aerodynamický tunel pro měření lopatkových mříží

Lopatkový kanál

Howell, A. R.

Carter, A. D. S.

Lieblein, S.

Japikse,1997

Dixon and Hall, 2010

Lopatkové kánaly v lopatkových strojích svůj tvar a velikost po délce mění, tak jak se mění profil a rozteč lopatek, které tyto kanály vymezují. Zejména u zkroucených lopatek dochází k velkým změnám nejen geometrických ale i aerodynamickým parametrům proudění, takže pro aerodynamické výpočty je nutné mít k dispozici velké množství měření. Měření aerodynamických veličin pro kombinaci tolika proměnných je časově i finančně nákladné a proto byly vyvinuty výpočtové metody predikce změny aerodynamických veličin profilů při změně některých parametrů, např. metoda Howelova, Carterova, Liebleinova...[Japikse, 1997, s. 5-14], [Dixon and Hall, 2010]. Tyto metody mají užitek především při snaze snížit potřebné množství měření při drobných změnách na profilu a profilové mříži.

Tlaková ztráta profilové mříže

Při proudění jakýmkoli kanálem lze indikovat tlakovou ztrátu, která vzniká zejména vnitřním tření pracovní tekutiny. V případě lopatkových kanálů, respektive lopatkových mříží je tlaková ztráta L_p definována jako rozdíl, o který se musí tlak za mříží p₂ snížit, aby rychlost za mříží W₂ byla stejná jako rychlost W_2is při proudění mříží beze ztrát při výstupním tlaku p_2is, viz Rovnice 4. Přičemž stav před mříží je předpokládán stejný pro oba případy.

4: Tlaková ztráta profilové mříže

L_p [Pa] tlaková ztráta; p_2is [Pa] tlak za mříží při proudění beze ztrát; p₂ [Pa] tlak za mříží při dosažení stejných rychlostí před a za mříží W_{1, 2}.

Profilová ztráta profilové mříže

Profilovými ztrátami profilové mříže se rozumí nežádoucí transformace energie (disipace energie) v pracovní tekutině, které vnikají při průtoku profilovou mříží. Mezi profilové ztráty patří zejména ztráty vnitřním třením, ztráty při odtržení proudu od profilu, ztráty při víření za odtokovou hranou a ztráty v rázové vlně při proudění vysokými rychlostmi. Suma těchto ztrát vytváří profilovou ztrátu mříže.

Víření

Odtoková hrana

Odtokové hrany lopatek nejsou ostré především z pevnostních důvodů, takže mezi proudy od sací a přetlakové stranách lopatek je mezera, ve které vznikají drobné víry kvůli odlišným rychlostí těchto proudů, viz Obrázek 6. Přičemž víry jsou typickým jevem zvyšující entropii tekutiny.

6: Vířením za odtokovou hranou

Rázové vlny

Kritické Machovo číslo

Rychlost proudění se podél profilu mění, takže i když před mříží nedosahuje proudění rychlosti zvuku, tak v mříži této rychlosti dosáhnout může nebo ji dokonce překonat při určité nátokové rychlosti, kterou označujeme jako kritického Machovo číslo profilové mříže. Při následném poklesu rychlosti zpět na podzvukovou může, za jistých podmínek, vzniknout rázová vlna. Podrobnosti o proudění v profilových mříží vysokou rychlostí jsou uvedeny v kapitole Aerodynamika profilových mříží ve stlačitelném prostředí v [Škorpík, 2023c].

Energetická bilance

Profilová ztráta profilové mříže je ekvivaletní entalpii, o kterou se musí snížit izoentropický rozdíl entalpií za mříži, aby rychlost na výstupu byla stejná jako v případě proudění beze ztrát, viz Obrázek 7.

7: Energetická bilance profilových ztrát lopatkové mříže

(a) situace v konfuzorové mříži; (b) situace v difuzorové mříži. h [J·kg^-1] entalpie; s [J·kg^-1·K^-1] entropie; p_s [Pa] celkový tlak; L_h [J·kg^-1] profilové ztráty. Index _is označuje změny stavu při proudění beze ztrát.

Součinitel vztlaku

Součinitel odporu

Profilová ztráta

Tlaková ztráta

Rovnice pro výpočet součinitele vztlaku a odporu a profilovou ztrátu profilové mříže (Rovnice 10) lze odvodit na základě předchozího obrázku a z tlakové ztráty. Tyto rovnice lze použít i obráceně k výpočtu tlakové ztráty na základě aerodynamických veličin. Přičemž Rovnice 10d pro součinitel vztlaku pro případ proudění beze ztrát C_L,is je odvozena z požadavku na zakřivení proudu a Rovnice 10b je odvozena ze skutečných hodnot aerodynamických součinitelů–pravé strany těchto rovnic se u dobře navržené profilové mříže rovnají.

10: Rovnice pro výpočet aerodynamických veličin profilové mříže

C_L,is [1] součinitel vztlaku pro případ proudění bez profilových ztrát; σ [1] hustota lopatkové mříže. Orientace kótování úhlů nátokové a výtokové rychlosti β₁, β₂ je stejná jako orientace úhlů β_m na Obrázku 9. Odvození rovnic je v Příloze 5.

Přenositelnost aerodynamiky rovinné lopatkové mříže na aerodynamiku diagonálních a radiální lopatkových mříží

Transformační rovnice

Nožička, 1967

Japikse,1997

V Úloze 2 je předvedená aplikace aerodynamických dat získaných při měření na rovinné lopatkové mříži na axiální lopatkovou mříž, ale tato data mohou být aplikována i na radiální a diagonální lopatové mříže. V takovém případě se tvar lopatek nerovinných mříží musí transformovat bod po bodu na rovinné mříže. Na Obrázku 11 je příklad transformace tvaru kruhové lopatkové mříže na rovinnou pomocí transformačních rovnic. Podobným způsobem lze transformovat i diagonální lopatkovou mříž [Nožička, 1967, s. 84], [Japikse, 1997, s. 7-24]. Stejně tak se musí transformovat tlakové a rychlostní pole naměřené na rovinné lopatkové mříži zpět do kruhových souřadnic postupem odvozeným v [Nožička, 1967, s. 84]. Tyto tranformační rovnice jsou odvozeny za zjednodušujícího předpokladu potenciálního proudění.

12: Weiningův součinitel

C_Lisolated [1] součinitel vztlaku osamocené desky. Vzorec má platnost přibližně do hodnoty 1/σ= 0,7, od této hodnoty lze vycházet z grafu uvedeného v [Lakshminarayana, 1996, s. 212]. Od hodnoty 1/σ=2,5 je součinitel K blízký hodnotě 1.

Větrné turbíny

Vrtule

Mimo Weinigova součinitele existují i jiné způsoby jak určit součinitel vztlaku profilu v mříži, jestliže jsou známy jeho parametry při jeho měření jako osamoceného profilu. Tyto způsoby se používají při výpočtu lopatkových mříží větrných turbín a vrtulí, více v článku Aerodynamika větrných turbín.

Součinitel odporu

Jestliže nebude docházet k odtrhávání proudu od profilu, lze očekávat, že sounitel odporu profilu v mříži C_D nebude tak citlivý na aerodynamickou interferenci jako součinitel vztlaku C_L. Takže aerodynamický výpočet takto navržené profilové mříže lze začít tak, že z hodnot součinitele vztlaku a odporu profilu lze podle Rovnice 10 pro součinitel vztlaku C_L a navržený úhel střední aerodynamické rychlosti β_m vypočítat součinitel vztlaku C_L,is atd., viz Úloha 4.

Základní profil

V případě profilů s vytvořených prohnutím základního profilu (obvykle profily s prohnutím větším než u leteckých profilů) lze při výpočtu sil na lopatku vycházet z vlastností výchozího základního profilu. Výpočet vychází z předpokladu, že po prohnutí se příliš nezmění součinitel odporu C_D profilu, takže na základě výpočtu odporu profilu v mříží D lze stanovit i další hodnoty sil podle Obrázku 9.

Úlohy

r_m [m] střední poloměr lopatek.

Odkazy