TERMODYNAMIKA TEPELNÝCH TURBÍN

– strana 13.3 –

● Úloha 546: Příklad výpočtu základní energetické bilance tepelné turbíny, viz čl. 1 ● Úloha 871: Výpočet expanze páry v parní turbíně ● Úloha 1000: Výpočet změny hmotnostního toku v tepelné turbíně při změně vstupního tlaku, viz čl. 15.

– strana 13.4 –

Polytropická expanze

– strana 13.5 –

Termodynamický návrh stupně tepelné turbíny

● Úloha 188: Výpočet přetlakového stupně ● Úloha 1036: Výpočet vnitřních ztrát stupně pomocí empirických vzorců, viz čl. 5. ● Úloha 1035: Výpočet axiálního stupně tepelné turbíny se zkroucenými lopatkami při uvažování ztrát, viz čl. 5.

– strana 13.12 –

Provedení chlazení lopatek a metody ke zvýšení jejich teplotní odolnosti

● Úloha 1144: Výpočet teplotní roztažnosti hřídele s nerovnoměrným teplotním zatížením, viz [Škorpík, 2025]

– strana 13.16 –

Odkazy

– strana 13.16-26 –

Přílohy

Zobrazení v PDF

– e-shop –

Jestliže byl článek pro vás užitečný, pak si kupte plnou verzi článku v mém e-shopu. Velmi vám za to děkuji a přeji, aby se vašim projektům dařilo.

Jiří Škorpík

autor

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.3

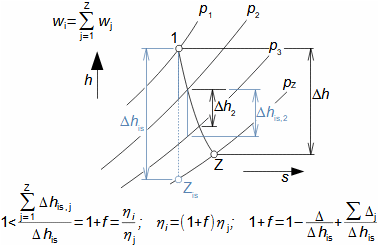
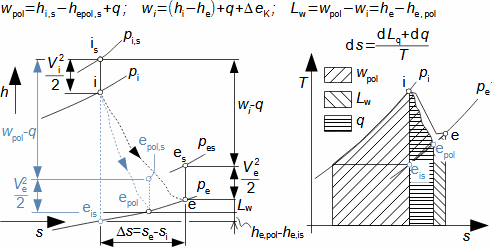
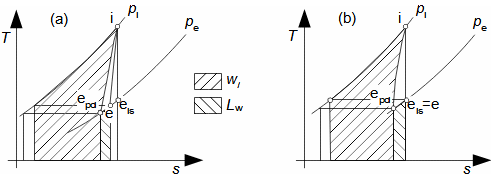
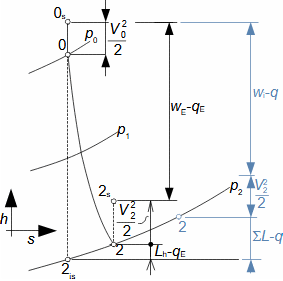
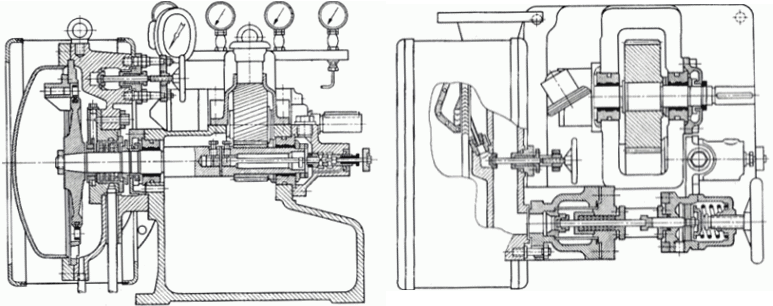
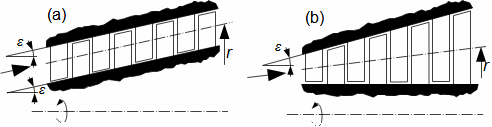
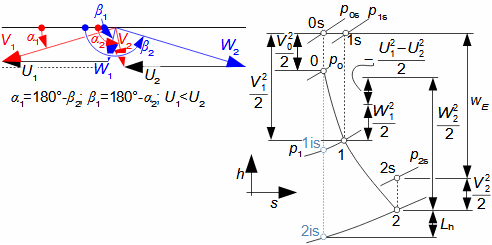
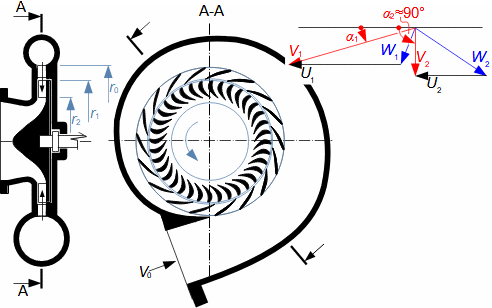
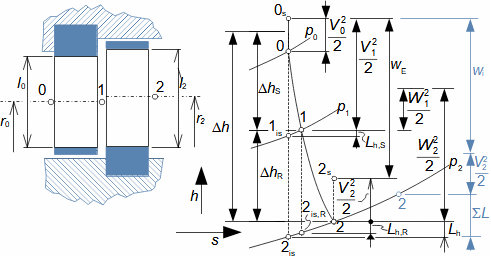
Expanze v tepelné turbíně

Charakteristickým rysem expanze plynu v turbíně je plynulost transformace vnitřní tepelné, tlakové, kinetické a případně potenciální energie na práci. Přitom se mění hustota i teplota a návrh stupně i energetická rovnováha vyžaduje speciální znalosti z konstrukce h-s i T-s diagramu. Obvykle je expanze spojená s vysokou teplotou, alespoň na vstupu, to klade další speciální požadavky, tentokrát na materiály lopatek a jejich chlazení.

Adiabatická expanze

Výpočtový model adiabatické expanze se používá v případech, při kterých se neočekává významný vliv sdílení tepla s okolím turbíny, i když je teplota expandujícího plynu vyšší než teplota okolí, ale jsou také dobře tepelně izolovány a expanze je příliš rychlá, než aby došlo k významnému vlivu sdílení tepla s okolím na expanzi.

1/2 Na obrázku je malá expanzní turbína pro klimatizace kabin dopravních letounů od společnosti Aviatron. Uvnitř expanduje vzduch odebraný z kompresorů hlavních motorů, expanzí se ochladí. pic.twitter.com/OPJ4waXBTg
— Jiří Škorpík (@jiri_skorpik) February 27, 2026

Definice ideální adiabatické expanze: Při adiabatické expanzi je ideální porovnávací změnou, která slouží k identifikaci ztrát, izoentropická expanze. Při ideální expanzi se obvykle očekává stejná výtoková rychlost jako při reálné expanzi. To znamená, že reálný stroj musí mít o něco větší průtočné průřezy než stroj ideální, protože ztrátové teplo měrný objem pracovního plynu zvětšuje.

Reálná adiabatická expanze: Charakteristickým rysem expanze v tepelné turbíně je také tzv. teplo znovu využité Δ. Jedná se o část ztrátového tepla ([Škorpík, 2024]) vzniklého disipací energie L_q, která v další části turbíny byla transformována na vnitřní práci. Na Obrázku 307 je příklad expanze v turbíně nebo jejím stupni v h-s a T-s diagramu. Zatímco v h-s diagramu lze odlišit pouze vnitřní ztráty jako celek, tak v T-s diagramu lze odlišit jednotlivé typy ztrát.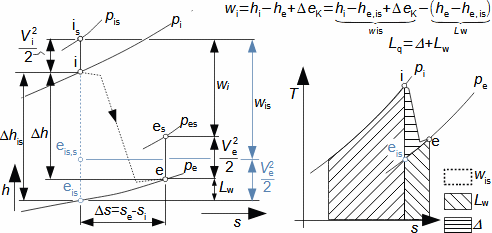

– 307: –

Adiabatická expanze v h-s a T-s diagramu

Vnitřní práce tepelné turbíny při adiabatické expanzi v h-s a T-s diagramu

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.4

h [J·kg^-1] entalpie; L_q [J·kg^-1] ztrátové teplo, respektive úhrn různých druhů energií transformovaných na vnitřní energii plynu v průběhu expanze; L_w [J·kg^-1] vnitřní ztráty na práci expanze; s [J·kg^-1·K^-1] entropie; T [K] absolutní teplota; w_is [J·kg^-1] vnitřní práce při izoentropické expanzi (adiabatická expanze beze ztrát); Δ [J·kg^-1] teplo znovu využité (část L_q, které bylo v jiné části turbíny transformováno na práci); Δe_K [J·kg^-1] rozdíl kinetické energie mezi vstupem a výstupem (obvykle nevýznamně velký rozdíl). Index _is označuje stavy při izoentropické kompresi, index _s celkový stav. T-s diagram je sestrojen při nevýznamném rozdílu kinetických energií. Rovnice jsou odvozeny v Příloze 307.

Rozbor vícestupňové adiabatické expanze v turbíně: Znovu využité teplo Δ přímo zvyšuje účinnost vícestupňové expanze proti jednostupňové expanzi, protože část tepla ze ztrátových procesů v předchozím stupni se využije při expanzi v následujícím stupni. To znamená, že vnitřní účinnost stupňové části vícestupňových turbín η_i je větší, než je střední vnitřní účinnost jednotlivých stupňů η_j, viz Obrázek 116.

– 116: –

Vícestupňová adiabatická expanze v turbíně

Z [-] počet stupňů; 1+f [1] součinitel zpětného využití ztrát (tzv. reheat coefficient, 1,02 až 1,04 podle [Kadrnožka, 1991]); η_i [1] vnitřní účinnost expanze mezi bod 1-Z. Index _j označuje j-tý stupeň. Rovnice jsou odvozeny pro předpoklad, že všechny stupně zpracovávají stejný entalpický spád a expanze je adiabatická. Pro přehlednost není v obrázku zakreslena kinetická energie absolutní rychlosti. Rovnice jsou odvozeny v Příloze 116.

– Úloha 871: –

Vypočítejte vnitřní výkon parní turbíny a suchost páry na konci expanze. Průtok páry turbínou je 33 t·h^-1, vnitřní účinnost turbíny je 75 %, měrná izoentropická práce turbíny je 1259,59 kJ·kg^-1, tlak na výstupu z turbíny je 3 kPa, tlak a teplota na vstupu do turbíny jsou 3,5 MPa, 450 °C. Řešení úlohy je uvedeno v Příloze 871.

Polytropická expanze

Výpočtový model polytropické expanze se používá v takových případech kdy je expanze ovlivněna teplem z okolí. To nastává například u radiálních turbín s velkou plochou disku, při chlazení teplotně exponovaných částí turbíny apod.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.5

Ideální vs. reálná polytropická expanze: Při polytropické expanzi bývá porovnávacím dějem obvykle vratná polytropická expanze. Polytropickou expanzi lze popsat Rovnicemi 685. Tyto rovnice lze odvodit z obecné rovnice prvního zákona termodynamiky.

– 685: –

Polytropická expanze při q>0

e_pol stav plynu na výstupu ze stroje při vratné polytropické expanzi. w_pol [J·kg^-1] vnitřní práce při vratné polytropické expanzi (expanze beze ztrát) při stejném rozložení sdíleného tepla q – sdílené teplo q musí mít na entropii a teplotu stejný dopad jako u reálného děje. Index _pol označuje vratnou polytropickou expanzi. T-s diagram je sestrojen při nevýznamném rozdílu kinetických energií. Postup konstrukce T-s diagramu je popsán v Příloze 685.

– 686: –

Polytropická expanze při q<0 (Chlazená expanze)

Vnitřní práce turbíny s chlazenou expanzí q<0

(a) případ, kdy t_e,is>t_e; (b) případ, kdy t_e,is=t_e (zdánlivě izoentropická expanze). T-s diagram je sestrojen při nevýznamném vlivu rozdílu kinetických energií.

Termodynamický návrh stupně tepelné turbíny

Pro termodynamický návrh stupně tepelné turbíny lze použít poznatky publikované v předchozích článcích tohoto sborníku (turbomachinery.education). Následuje tedy shrnutí a doplnění některých speciálních poznatků týkající se termodynamiky stupňů tepelných turbín: h-s diagramy stupňů; obvyklé hodnoty podobnostních součinitelů; stupně tepelných turbín s přímými lopatkami; stupně tepelných turbín se zkroucenými lopatkami; kuželové stupně a stupně radiálních turbín.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.6

~ h-s diagramy stupňů tepelných turbín: Na Obrázek 908 je h-s diagram stupně tepelné turbíny na vyšetřovaném poloměru pro vyšetření Eulerovy práce. V případě polytropické expanze nelze zakreslit do diagramů jednotlivé kinetické energie, protože entalpie jsou ovlivněny teplem q. Modře je vyznačena energetická rovnováha celého stupně.

– 908: –

h-s diagram expanze ve stupni tepelné turbíny

L_h [J·kg^-1] profilové ztráty; ΣL [J·kg^-1] celkové ztráty stupně; V [m·s^-1] absolutní rychlost; q_E [J·kg^-1] teplo sdílené v okolí vyšetřované proudnice.

~ Obvyklé hodnoty podobnostních součinitelů: Maximální účinnosti Eulerovy práce dosahují axiální stupně tepelných turbín při hodnotě průtokového součinitele kolem 0,65 a tlakového součinitele 2,5-2,6 [Smith, 1965], [Dixon and Hall, 2010, s. 119].

~ Obecné vlastnosti stupňů s přímými lopatkami: Axiální stupně s přímými lopatkami se používají jako levnější alternativa ke stupňům se zkroucenými lopatkami zejména v případě velmi malých poměrů délky lopatek ku střednímu průměru lopatek, tedy v případech, kdy prostorový charakter proudění není tolik výrazný a je adekvátní použití 1D výpočet lopatky. Samozřejmě je nutné očekávat nižší účinnost takových stupňů oproti stupňům se zkroucenými lopatkymi. Stupně s přímými lopatkami se používají u parních turbín, které se vyrábějí kusově.

Obvyklé stupně reakce stupňů s přímými lopatkami: Stupně s přímými lopatkami se navrhují, buď rovnotlakové se stupněm reakce blízkým 0, nebo jako přetlakové se stupněm reakce 0,5. Z pohledu termodynamických vlastností lze rozdíly mezi těmito dvěma typy stupňů vyčíst z jejich bezrozměrových charakteristik ψ-ϕ. Respektive u rovnotlakového stupně lze očekávat dvakrát větší vnitřního práci než u stupně přetlakového při stejné délce a středního poloměru lopatek a stejných otáčkách. Na druhou stranu bezrozměrová charakteristika rovnotlakového stupně bude strmější než u přetlakového atd.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.7

Konstrukce rovnotlakového stupně s přímými lopatkami: Na Obrázku 350 je typické provedení rovnotlakového stupně se stupněm reakce cca 0,03 až 0,05 a jeho rychlostní trojúhelník podle [Kadrnožka, 2004, s. 91]. Stupeň reakce by měl být takový, aby přinesl snížení profilových ztrát, které jsou funkcí rychlostí, ale současně zůstaly zachovány výhody rovnotlakové koncepce stupně. Rovnotlakové stupně lze konstruovat i se zkroucenými lopatkami (snížení ztráty nesprávným nátokovým úhlem po délce lopatek), ale v takovém případě jsou lopatky zkroucené výrazně více než při proměnném stupni reakce pod délce lopatek.

– 350: –

Rovnotlakový axiální stupeň s malým stupněm reakce

Sh-bandáž (shroud); LS-labyrintová ucpávka (labyrinth seal). A [m²] průtočná plocha lopatkového kanálu; b [m] šířka lopatkové mříže; l [m] délka; L_D [kg·s^-1] odvod pracovní tekutiny z mezery mezi disky (jedná se o ztrátu); r [m] poloměry lopatek (index _t označuje špici lopatek, index _h označuje patu lopatek); U [m·s^-1] obvodová rychlost; W [m·s^-1] relativní rychlost; α [°] úhel absolutní rychlosti; β [°] úhel relativní rychlosti; γ [°] úhel nastavení profilu v lopatkové mříži; δ [m] velikosti axiálních mezer.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.8

Konstrukce přetlakového stupně s přímými lopatkami: Na Obrázku 353 je válcový řez přetlakovým a jeho rychlostní trojúhelník pro stupeň reakce R=0,5. Při takové reakci jsou nejnižší profilové ztráty, protože rychlosti V₁ a W₂ jsou stejné nebo velmi podobné. Odtud plyne i symetrický tvar rychlostního trojúhelníku pro statorovou a rotorovou řadu lopatek (Úloha 188, s. 13.9) a tedy je možné použít stejného tvaru lopatek pro statorovou i rotorovou řadu, což je výrobně výhodné. Zvětšení délky lopatek na výstupu je dáno požadavkem na zachování meridiánové rychlosti při poklesu hustoty při expanzi.

– 353: –

Válcový řez přetlakovým stupněm a jeho rychlostní trojúhelník

Na obrázcích nejsou prokresleny závěsy.

Zjednodušený výpočet profilových ztrát přímých lopatek: Typické pro parní turbíny s přímými lopatkami je také zjednodušená predikce velikosti profilových ztrát pomocí teorie trysek místo použití aerodynamických dat profilových mříží. Tato predikce spočívá v přirovnání lopatkového kanálu k trysce, i když zakřivené, pak lze predikovat změnu výtokové rychlosti z kanálu a tedy profilovou ztrátu pomocí rychlostního součinitele (viz článek Proudění plynů a par tryskami [Škorpík, 2023]), tak jak je zobrazeno na Obrázku 178.

– 178: –

Hodnoty rychlostních součinitelů lopatkových mříží parních turbín

a-přetlaková mříž (stupeň reakce 0,5); b-rovnotlaková mříž. Δβ [°] zakřivení proudu v mříži; φ [1] rychlostní součinitel ve statorovém kanále; ψ [1] rychlostní součinitel v rotorovém kanále. Index ₁ označuje parametry před rotorovou řadou lopatek, index ₂ označuje parametry za rotorovou řadou lopatek, index _S označuje statorovou řadu lopatek, index _R označuje rotorovou řadu lopatek. Zdroj dat [Krbek, 1990, s. 82].

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.9

– Úloha 188: –

Navrhněte délky přímých lopatek, rychlostní trojúhelníky a vypočítejte axiální sílu působící na rotor přetlakového stupně parní turbíny. Průtok páry stupněm je 12 kg·s^-1, otáčky rotoru 50 s^-1, tlak páry na vstupu do statoru 1,25 MPa při teplotě 320 °C, střední průměr délky lopatek je 650 mm, stupeň reakce 0,5, úhel absolutní rychlosti na výstupu ze statoru je 20°, rychlostní součinitel statoru i rotoru je stejný 0,93 a po celé výšce lopatky konstantní. Izoentropický spád stupně musí být 21,3 kJ·kg^-1. Proveďte porovnání tlakového součinitele s tlakovým součinitelem pro ideální přetlakový stupeň. Zadání úlohy je převzato z [Krbek, 1990 s. 110]. Řešení úlohy je uvedeno v Řešení úlohy je uvedeno v Příloze 188.

Stanovení hustoty lopatkových mříží s přímými lopatkami: Střední čára profilu tepelných turbín s přímými lopatkami bývá velmi prohnutá. Optimální hustotu lopatkových mříží s takovými lopatkami lze určit pomocí Zweifelova součinitele.

Hmotnostní tok lopatkovým kanálem s přímými lopatkami: Teorii trysek lze využít i při stanovení součinitele průtoku μ lopatkovým kanálem. Například v [Kadrnožka, 2004, s. 110] jsou uvedeny hodnoty součinitele průtoku pro různé případy proudění v lopatkových mříží.

Curtisův stupeň s přímými lopatkami: Speciálním případem rovnotlakového stupně je Curtisův stupeň. V tomto případě se disponibilní energie transformuje na kinetickou energii ve statorové řadě lopatek, ale potom proudí více jak jednou řadou lopatek rotorových, mezi kterými je vložena další rovnotlaková statorová lopatková řada, která pouze mění směr proudění, viz Obrázek 913, s. 13.10. Podle toho kolik takový stupeň obsahuje rotorových řad se nazývá Curtisův dvouvěncový, třívěncový stupeň atd. Curtisův jednověncový stupeň je klasický axiální rovnotlaký stupeň. U velmi malých parních turbín lze použít i obracecí kanál, čímž pára projde rotorovou řadou lopatek dvakrát, viz Obrázek 914, s. 13.10.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.10

– 913: –

Válcový řez Curtisovým stupněm a jeho rychlostní trojúhelník

Rychlostní trojúhelník na tomto obrázku je pro případ ideálního proudění bez profilových ztrát. w_C [kJ·kg^-1] Eulerova práce ideálního Curtisova dvouvěncového stupně; w_R=0 [kJ·kg^-1] Eulerova práce ideálního rovnotlakového stupně. Odvození uvedených rovnic je v Příloze 913.

– 914: –

Jednostupňová parní turbína pro nízký průtok a vysoký entalpický spád

Parní turbína pro nízký průtok a vysoký entalpický spád: Turbína je konstruována jako Curtisův dvouvěncový stupeň. Turbína obsahuje pouze jednu Lavalovu trysku. Místo druhé statorové řady je obracecí kanál, který přivádí páru zpět na první rotorovou řadu. Obrázek z [Miller et al. 1972].

Na obrázku je dvouvěncový Curtisův stupeň pohonu turbočerpadel německé raketové střely V-2 (A-4). Výkon kolem 50 kW při otáčkách 3800 až 4000 rpm. Směr vodní páry a dalších plynu se vyráběla reakcí H2O2 a NaMnO4–dodnes užívané na Sojuzech, jehož motory jsou vylepšené motory V-2. pic.twitter.com/jmIvIPf97d
— Jiří Škorpík (@jiri_skorpik) April 5, 2023

Porovnání jednotlivých typů stupňů s přímými lopatkami: Curtisův dvouvěncový stupeň za stejných podmínek dokáže zpracovat větší rozdíl entalpií ve stupni než rovnotlakový nebo přetlakový stupeň (v poměrech 8:2:1 jak plyne z výše uvedených odstavců), ale za cenu horší vnitřní účinnosti, protože rychlosti, a tedy i profilové ztráty, jsou velmi vysoké. Pro zvýšení vnitřní účinnosti na středním poloměru Curtisova stupně se konstruují jednotlivé lopatkové řady s mírným přetlakem.

Použití jednotlivých typů stupňů s přímými lopatkami: Rovnotlakové stupně se používají u jednostupňových turbíny tzv. Lavalových turbín i u vícestupňových parních a plynových turbín. Curtisova stupně se používají tam, kde je důraz na vysoký výkon v malém objemu. Dvouvěncový Curtisův stupeň byl hnací turbínou turbočerpadel raketového motoru německé raketové střely V-2 o výkonu 50 kW, stejně tak je nalezneme i v ruských raketových motorech RD 108 pro pohon Sojuzů apod. Přetlakové stupně jsou častější u vícestupňových parních turbín s důrazem na jednoduchost a menší pořizovací nároky.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.11

~ Zkroucené lopatky: Termodynamický návrh axiálního stupně tepelné turbíny v provedení se zkroucenými lopatkymi je uveden již v úloze v článku Vnitřní ztráty lopatkových strojů a jejich vliv na návrh lopatkového stroje. Přičemž v uvedeném článku je popsán i postup při výpočtu stupně reakce po výšce lopatek a typy ztrát, se kterými je nutné počítat.

~ Obecné důvody pro stavbu Kuželových stupňů: V kuželových stupních se mění průtočný průřez změnou výšky hran lopatek tak, aby při expanzi plynu byla zachována meridiální rychlost. Kuželové stupně bývají v provedením se zkroucenými lopatkami i s přímými lopatkami. h-s diagram kuželového stupně na vyšetřovaném poloměru je totožný s diagramem radiálního stupně.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.12

~ Obecné důvody pro stavbu Radiálních stupňů: Radiální stupně se používají jako dražší ale účinější jednostupňová alternativa k rovnotlakových a Curtisovým stupňům, protože Eulerovu práci radiálního stupně zvyšuje rozdíl obvodových rychlostí a tak rychlosti proudění mohou být nízké i při velkých entalpických spádech. Používají se například u turbodmychadel a turboexpandérů. Okrajově se vyrábí i radiální turbíny tepelných turbín s přímými lopatkymi, viz Obrázek 393. Tyto stupně nejsou vhodné pro vodní páru s jakýmkoliv podílem vlhkosti, jelikož vodní kapky působením odstředivých sil proudí centrifugálně.

– 393: –

Radiální jednostupňová parní turbína

Stupeň reakce Radiálních turbín: Radiální stupně se musí navrhovat alespoň s minimálním stupněm reakce a to i rovnotlakové. Například u turbín (centripetální stupeň) by při nulovém stupni reakce došlo vlivem odstředivých sil, ke zpomalování relativní rychlosti na výstupu z rotorové řády a tedy ke zmenšení Eulerovy práce. Minimální stupeň reakce centripetální turbín lze stanovit dosazením podmínky W₁=W₂.

Provedení chlazení lopatek a metody ke zvýšení jejich teplotní odolnosti

Vysoká teplota pracovního plynu umožňuje dosáhnout i vysoké tepelné účinnosti oběhu, ve kterém turbína pracuje. Nicméně to klade vysoké nároky na materiál lopatek a jejich povrchovou úpravu. Další možností je chlazení lopatek.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.13

~ Reakce materiálu lopatek na růst teploty: Při vysokých teplotách se snižuje pevnost oceli a zvyšuje citlivost na korozi – vliv teploty na tyto parametry materiálu se označuje jako teplotní odolnost. Pevnost oceli při vysoké teplotě lze zajistit různými příměsi v materiálu lopatek jak ukazuje Obrázek 1001, na kterém jsou zobrazeny potřebné příměsi v oceli podle požadované provozní teploty lopatky. Složení slitin ocelí pro rotory a lopatky tepelných turbín pro vysoké teploty jsou uvedeny v [Beneš et al., 1974, s. 194], [Koutský, 2005, s. 61], [Škopek, 2007, Příloha 20].

– 1001: –

Potřebné příměsi oceli podle provozní teploty

Potřebné příměsi materiálu lopatek podle provozní teploty

t [°C] provozní teplota lopatek. Podle údajů z [Anon., 2014].

Negativní vlivy příměsí v materiálech lopatek: Použití příměsi má zlepšit především teplotní odolnost, ale obvykle se tím zhorší jiné vlastnosti oceli, například odolnost proti otěru, proto se na takové lopatky navařuje pomocí laseru ochranná vrstva z tvrdšího kovu [Míšek, 2014]. Například na Obrázku 782 je lopatka parní turbíny ze slitiny oceli a titanu, který snižuje hustotu lopatky a tedy i napětí od odstředivé síly (na obrázku je lopatka ještě bez ochranné vrstvy), snižuje odolnost povrchu proti otěru.

– 782: –

Lopatka parní turbíny ze slitiny oceli a titanu

Lopatka posledního stupně parní turbíny o délce 1375 mm společnosti Doosan Škoda Power.

Materiály lopatek s keramickou matricí: Pro zvýšení vysokoteplotní odolnosti lopatek (snížení vlivu creepu) se také používají kompozitní materiály s keramickou matricí (CMC ceramic matrix composite). Tento materiál má také relativně nízkou hustotu, což snižuje napětí v lopatce od odstředivých sil [Hocko, 2012, s. 55].

Do you know what goes into the composition of CMCs (Ceramic Matrix Composites)? We’re breaking it down in 27 seconds or less! pic.twitter.com/dJbUWsNwV7
— GE Aerospace (@GE_Aerospace) June 13, 2024

Korozní odolnost materiálů lopatek: Povrchovou úpravou, jako je leštění, lze zase zvýšit korozní odolnost. Zvláště při vysokých teplotách za přítomnosti kyslíku hrozí zvýšená tvorba okujení (tvorba tvrdých oxidů – rez).

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.14

~ Způsoby chlazení lopatek: Pokud nestačí vysoká jakost materiálů, je nutné lopatky tepelných turbín aktivně chladit, zejména u prvních stupňů. To zahrnuje chlazení závěsů, lopatek s chladicími kanálky (Obrázek 682) nebo chlazení filmem studeného plynu, který je drobnými otvory na přetlakové případně sací straně vháněn do mezní vrstvy kolem lopatky apod. Jako chladící médium se používá vzduch (spalovací turbíny) nebo voda (Parní turbíny) [Miller et al., 1972, s. 931]. Některé zajímavé koncepty chlazení lopatek z ranných dob vývoje spalovacích turbín, které se ovšem neosvědčily jsou uvedeny v [Dokoupil, 2015, s. 221].

Chlazení lopatek vzduchem: Při chlazení vzduchem musí být povrchy chladícíh kanálů ošetřeny antikorozní vrstvou. V případě spalovacích turbín je vzduch pro chlazení odebírán v její kompresorové části v místě, kde je tlak o něco vyšší než v okolí chlazené lopatky. Chladící vzduch z lopatky proudí otvory v odtokové hraně lopatky do proudu spalin. Efektivitu chlazení zvyšuje vnější povrchová vrstva lopatek s nízkou hodnotou teplotní vodivostí, například keramické nástřiky apod.

– 682: –

Lopatky spalovací turbíny řady MS5002 od GE s chladícími kanály [Anon., 2011]

Snížení počtu chlazených lopatek pomocí prudké expanze v první stupni: Pro rozdělení entlapického spádu v tepelné turbíně je typické, že první stupně jsou navrženy tak, aby zpracovaly větší entalpický spád než další stupně. To sice může zhoršit termodynamickou účinnost prvních stupňů, ale klesne tím počet lopatek pracujících v oblasti vysokých teplot a tedy i cena turbíny – takové rozložení entalpických spádu je běžné u parních turbín.

TERMODYNAMIKA TEPELNÝCH TURBÍN

strana 13.15

Odkazy

ŠKORPÍK, Jiří, 2023, Proudění plynů a par tryskami, fluid-dynamics.education, Brno, https://fluid-dynamics.education/proudeni-plynu-a-par-tryskami.html.

ŠKORPÍK, Jiří, 2024, Technická termomechanika, engineering-sciences.education, Brno, https://engineering-sciences.education/technicka-termomechanika.html.

ŠKORPÍK, Jiří, 2025, Meze použití materiálů, engineering-sciences.education, Brno, https://engineering-sciences.education/meze-pouziti-materialu.html.

ANON., 2011, MS 5002 Gas Turbine a Through D Evolution, ge.com.

ANON., 2014, Co nám může v budoucnosti nejvíc chybět? Na čem jsem závislí, Technický týdeník, 01/2014, Business Media CZ, Praha, ISSN 0040-1064.

BENEŠ, Antonín, DRASTÍK, František, HOSTINSKÝ, Zdeněk, KOUTSKÝ, Jaroslav, NĚMEC, Josef, 1974, Nauka o kovech, SNTL, Praha.

DIXON, S., HALL, C., 2010, Fluid Mechanics and Thermodynamics of Turbomachinery, Elsevier, Oxford, ISBN 978-1-85617-793-1.

DOKOUPIL, Eduard, 2015, Turbíny pro Luftwaffe: zrod a popis prvních německých proudových motorů, Dokoupil Eduard, Světlá, ISBN 978-80-260-8153-1.

HOCKO, Marián, 2012, Transformace leteckých lopatkových motorů na spalovací turbíny, Západočeská univerzita v Plzni, Plzeň, ISBN 978-80-261-0218-2.

KADRNOŽKA, Jaroslav, 1991, Teorie lopatkových strojů, Vysoké učení technické v Brně, Brno, ISBN 80-214-0275-X.

KADRNOŽKA, Jaroslav, 2004, Tepelné turbíny a turbokompresory, Akademické nakladatelství CERM, s.r.o., Brno, ISBN 80-7204-346-3.

KOUTSKÝ, Jaroslav, 2005, Development and application of Original Special Steels-Base of World Famous Level of Skoda-Works Steam turbines, Energetické stroje-termomechanika-mechanika tekutin , Fakulta strojní Západočeské university v Plzni, Plzeň.

KRBEK, Jaroslav, 1990, Tepelné turbíny a turbokompresory, Vysoké učení technické v Brně, Brno, ISBN 80-214-0236-9.

MILLER, Rudolf, HOCHRAINER, A., LÖHNER, K., PETERMANN, H., 1972, Energietechnik und Kraftmaschinen, Rowohlt taschenbuch verlag GmbH, Hamburg, ISBN 3-499-19042-7.

MÍŠEK, Tomáš, 2014, Vývoj ultra dlouhé lopatky Doosan Škoda Power pro kondenzační parní turbíny, Technický týdeník, 10/2014, Business Media CZ, Praha, ISSN 0040-1064.

POLSTER, Burkard, 2014, Q.E.D. Krása matematického důkazu, Dokořán s.r.o., Praha, ISBN 978-80-7363-532-9.

ŠKOPEK, Jan, 2007, Parní turbína-tepelný a pevnostní výpočet, Západočeská univerzita v Plzni, Plzeň, ISBN 978-80-7043-256-3.

SMITH, F., 1965, A simple correlation of turbine efficiency, Journal of the Royal Aeronautical Society, 69, 467–470.

– e-shop –

Jestliže byl článek pro vás užitečný, pak si kupte plnou verzi článku v mém e-shopu. Velmi vám za to děkuji a přeji, aby se vašim projektům dařilo.

Jiří Škorpík

autor