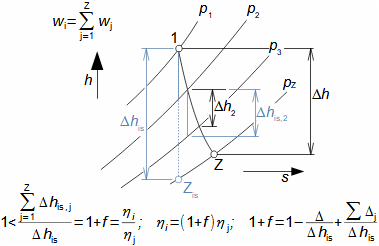
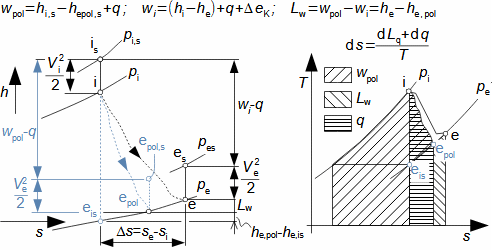
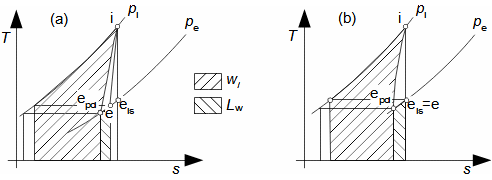
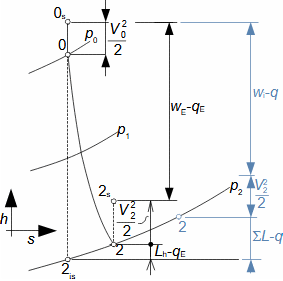
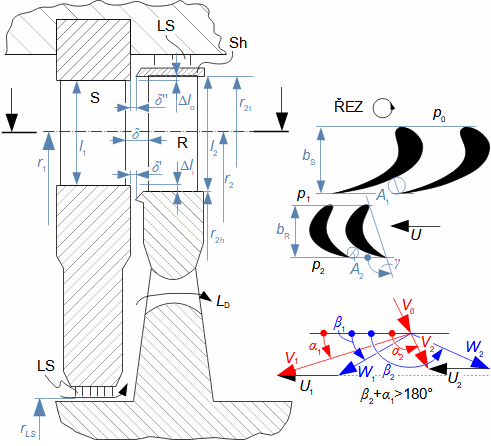
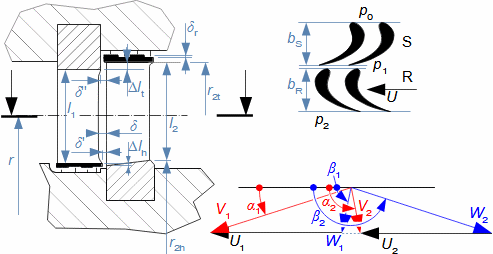
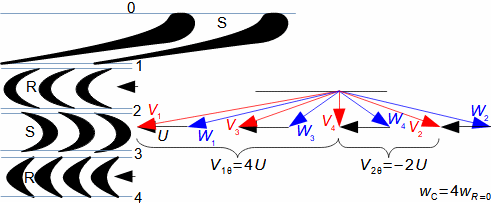
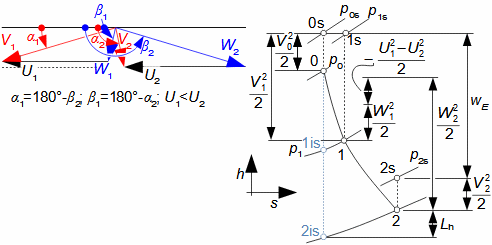
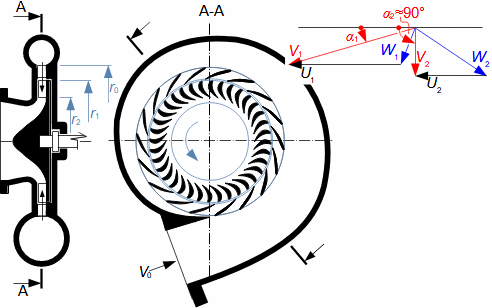
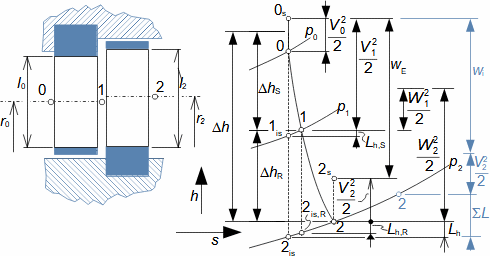
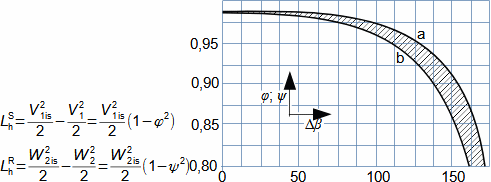Thermodynamics of heat turbines

Transformační technologie (transformacni-technolgie.cz; fluid-dynamics.education; turbomachinery.education; engineering-sciences.education; stirling-engine.education)

ISSN:

1804-8293

Chapter: Expansion in heat turbine

13.3

Expansion in heat turbine

Gas expansion in turbines smoothly transforms internal thermal, pressure, kinetic, and potential energy into work. Density and temperature change, necessitating knowledge of h-s and T-s diagram design for energy balance calculation.

Usually the expansion is associated with high temperature, at least at the inlet this puts additional special requirements, this time on the blade materials and their cooling.

Adiabatic expansion

Outlet velocity

Comparative change^1.

In adiabatic expansion, isentropic expansion serves as the ideal comparative change, identifying losses. In ideal expansion, the same exit velocity is usually expected as in actual expansion. This means that the real machine must have larger flow areas than the ideal machine because the loss heat increases the specific volume of the working gas.

Heat transfer

The adiabatic expansion computational model is used in cases where the turbine is not expected to have a significant heat transfer to the surrounding, even if the temperature of the expanding gas is higher than the surrounding temperature, but they are also well thermally insulated and the expansion is too fast to have a significant heat transfer effect on the expansion.

Re-usable heat

h-s diagram

T-s diagram

Internal losses^1.

Internal work^1.

Loss heat

A characteristic feature of expansion in a heat turbine is also the so-called re-usable heat Δ. This is a part of the loss heat ([Škorpík, 2024]) generated by dissipation of energy L_q, which was transformed into internal work in another part of the turbine. Figure 1 shows an example of expansion in a turbine or in a single stage in the h-s and T-s diagrams. While in the h-s diagram only the internal losses as a whole can be identified, in the T-s diagram the individual types of losses can be identified.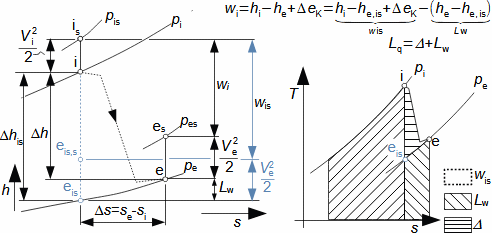

1: Internal work of heat turbine at adiabatic expansion in h-s and T-s diagrams

Chapter: Adiabatic expansion

13.4

h [J·kg^-1] enthalpy; L_q [J·kg^-1] loss heat, or sum of different types of energy transformed into internal energy of gas at expansion process; L_w [J·kg^-1] internal losses; s [J·kg^-1·K^-1] entropy; T [K] absolute temperature; w_is [J·kg^-1] internal work at isentropic expansion (adiabatic expansion with no losses); Δ [J·kg^-1] re-usable heat (part of L_q that has been transformed into work in another part of turbine); Δe_K [J·kg^-1] difference in kinetic energy between inlet and outlet (usually insignificantly large difference). The index _is denotes the isentropic compression states, the index _s the stagnation state. The T-s diagram is constructed when the kinetic energy difference is insignificant. The equations are derived in Appendix 3.

Multi-stage expansion

Reheat factor

The Re-usable heat Δ directly increases the efficiency of multi-stage expansion compared to single-stage expansion, because part of the heat from the loss processes in the previous stage is used in the expansion of the next stage. This means that the internal efficiency of the stage part of multi-stage turbines η_i is greater than the mean internal efficiency of the individual stages η_j, see Figure 2.

2: Multi-stage adiabatic expansion in the turbine

Z [-] ] number of stages; 1+f [1] reheat factor (1.02 to 1.04 according to [Kadrnožka, 1991]); η_i [1] internal expansion efficiency between point 1-Z. The index _j denotes the j-th stage. The equations are derived for the assumption that all stages process the same enthalpy gradient and the expansion is adiabatic. For clarity, the absolute velocity kinetic energy is not plotted in the figure. The equations are derived in Appendix 4.

Polytropic expansion

Polytropic ideal expansion

Heat transfer

The computational model of polytropical expansion is used in cases where the expansion is affected by heat transfer with surrounding. This occurs, for example, in radial turbines with large disk area, in cooling of thermally exposed parts of the turbine, etc. In polytropic expansion, the comparative process is usually reversible polytropic expansion. Polytropic expansion can be described by Equations 3. These equations can be derived from the general equation of the first law of thermodynamics.

Chapter: Polytropic expansion

13.5

3: Turbine internal work for case q>0

e_pol state of gas at the machine outlet during reversible polytropic expansion. w_pol [J·kg^-1] internal work during reversible polytropic expansion (expansion without losses) at same heat transfer with surrounding q - heat q must have the same impact on entropy and temperature as in the actual process. The index _pol denotes reversible polytropic expansion. The T-s diagram is constructed when the difference of kinetic energies is insignificant. The procedure for constructing the T-s diagram is described in Appendix 5.

Cooled expansion

Figure 4 shows examples for cooled expansion (q<0).

4: Internal work of a turbine with cooled expansion q<0

(a) case when t_e,is>t_e; (b) case when t_e,is=t_e (apparently isentropic expansion). The T-s diagram is constructed when the effect of the kinetic energy difference is insignificant.

Kapitola: Thermodynamic calculation of heat turbine stage

13.6

Thermodynamic calculation of heat turbine stage

For thermodynamic calculations of the heat turbine stage, findings from previous articles in these proceedings can be utilized. Here, only special knowledge on heat turbine stage thermodynamics is summarized and supplemented.

h-s diagrams

Euler work^2.

Profile losses^4.

Total losses^5.

Figure 5 shows the h-s diagram of the heat turbine stage at the investigated radius for Euler work caculation. In the case of polytropic expansion, the individual kinetic energy cannot be plotted in the diagrams because the enthalpies are affected by the heat q. The energy balance of the whole stage is shown in blue.

5: h-s diagram of expansion in heat turbine stage

L_h [J·kg^-1] profile losses;ΣL [J·kg^-1] total losses of stage; V [m·s^-1] absolute velocity; q_E [J·kg^-1] heat transferred in the surroundings of the streamline under investigation.

Straight blades

Axial stage

1D calculation^1.

Axial stages with straight blades are used as a cheaper alternative to stages with twisted blades, especially in the case of very small ratios of blade length to mean blade diameter [Kadrnožka, 2004, p. 153], i.e. in cases where the spatial character of the flow is not so significant and the use of 1D blade claculation is adequate. Of course, lower efficiency of such stages compared to stages with twisted blades is to be expected. Straight blade stages are used in steam turbines which are manufactured in pieces.

Kapitola: Thermodynamic calculation of heat turbine stage

13.7

Impulse stage^2.

Reaction stage^2.

Reaction^2.

Dimensionless characteristic^6.

Straight blade stages are designed with the reaction close to 0 (impulse stages) or with the reaction 0.5 (reaction stages). From the point of view of thermodynamic properties, the differences between these two types of stages can be seen from their dimensionless ψ-ϕ characteristics. Respectively, the impulse stage can be expected to do twice as much internal work as the reaction stage for the same blade length and mean radius and the same rotor speed. On the other hand, the dimensionless characteristic of the impulse stage will be more abrupt than that of the reaction stage, etc.

Impulse stage

Profile losses

Velocity triangle^1.

Figure 6 shows a typical impulse stage design with reaction of approximately 0.03 to 0.05 and its velocity triangle according [Kadrnožka, 2004, p. 91]. The reaction should be such that it yields a reduction in profile losses, which are a function of velocity, while retaining the benefits of the impulse stage design.

6: Cylindrical cut through axial impulse stage with small reaction and its velocity triangle

Sh-shroud; LS-labyrinth seal. A [m²] flow area of blade passage; b [m] width of blade row; l [m] length; L_D [kg·s^-1] discharge of working fluid from gap between discs (it is loss); r [m] radii of blades (index _t denotes tip of blades, index _h denotes root of blades); U [m·s^-1] blade speed; W [m·s^-1] relative velocity; α [°] angle of absolute velocity; β [°] angle of relative velocity; γ [°] stagger angle; δ [m] sizes of axial gaps.

Kapitola: Thermodynamic calculation of heat turbine stage

13.8

Reaction stage

Symmetric blades

Meridian velocity^1.

Figure 7 shows a cylindrical section of the reaction stage and its velocity triangle for reaction R=0.5. In such the reaction, the profile losses are the lowest because the velocities V₁ and W₂ are the same or very similar. Hence the symmetrical shape of the velocity triangle for the stator and rotor blade rows and hence the same blade shape can be used for both stator and rotor rows, which is advantageous for manufacturing. When the symmetry of the velocity triangles is maintained, the condition V_2θ=0 cannot usually be met, see Problem 2. The increase in blade length at the outlet is due to the requirement to maintain the meridional velocity as the density decreases during expansion.

Cylindrical cut through axial reaction stage and its velocity triangle

7: Cylindrical cut through axial reaction stage

The blade roots are not drawn in the pictures.

Profile losses