SHAPES OF BLADES AND FLOW PARTS OF TURBOMACHINES

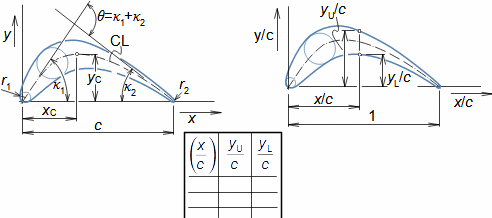
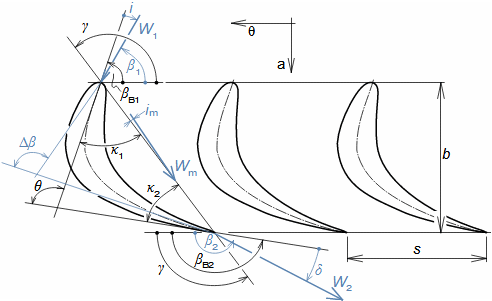
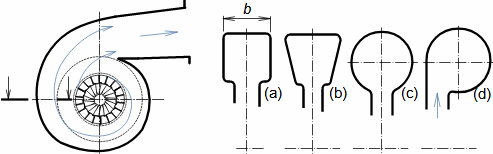
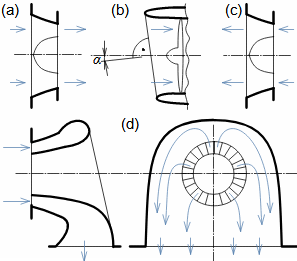
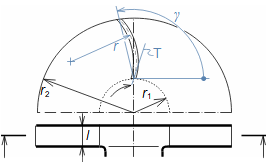
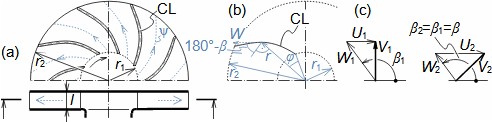
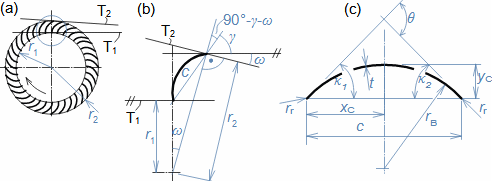
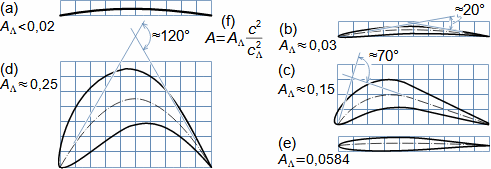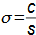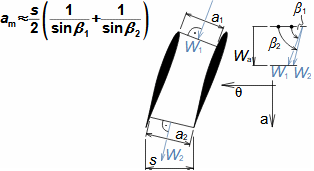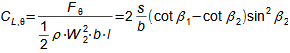Types of profile cascades

Stagger angle

Confuser cascade

Pressureless cascade

Diffuser cascade

The type of a profile cascades is determined by the stagger angle (inclination in the cascade). The size of the inlet and outlet flow area of a cascade is essential for the resulting velocities of the working fluid when flowing through the profile cascade. Any basic type of profile cascades with the same pitch can be constructed from the same profile by simply turning the profile or changing the stagger angle of the profile in the cascade, see Figure 1: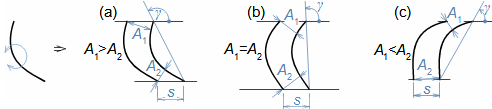

1: Relationships between basic types of profile cascades

(a) confuser cascade - also called overpressure, turbine cascades; (b) pressureless cascade - with same flow area pressure and velocity between inlet and outlet do not change; (c) diffuser cascade - also called overpressure, compressor or turbine cascades in case A₁ is critical flow area. A [m²] flow area. γ [°] stagger angle of profile in cascade; s [m] pitch. The profiles are simplistically drawn as if they were made of sheet.

Blade profile

The profile of the blade means its outline on a particular section. This chapter describes the methods for creating the blade profile drawing and the rules for determining the shape of the blade profile.

Profile drawing

Profile coordinates

Camber line

Chord

The blade profile can be recorded using blade profile geometry rules. The choice of the method of recording the blade profile shape depends on the medium of this recording, or the most suitable method in relation to the required form of production documentation. Currently, graphical output (using vector graphics) is sufficient, e.g. in CAD systems, as machine tools and computing software are able to work directly with such output, but other forms of blade profile notation exist. For example, they are written in tabular form in the x; y coordinates and using the shape of the camber line of the profile, see Figure 2.

Airfoils

Abbott and Doenhoff, 1959

A suitable profile can be selected from profile catalogues based on aerodynamic requirements. The shapes and aerodynamic data of thin and low camber profiles can be obtained from extensive airfoil catalogues used in aeronautics, for example [Abbott and Doenhoff, 1959]. If a suitable blade profile is missing from the catalog, it must be developed and experimentally verified.

Base airfoil

The development of a new profile is usually based on different camber of the so-called base airfoil, which is a symmetrical smooth airfoil, see Figure 3. There are many base airfoils differing from each other in shape, aerodynamic characteristics and other properties, see for example [Abbott and Doenhoff, 1959]. The development of a new profile resulting from the cambering of a base airfoil makes it possible to systematically define the aerodynamic differences between different camber and to clearly catalogue these new profiles according to the base airfoil they are based on.

3: Profile resulting from camber of basic airfoil

Strength

Profile cross-section

Camber line

In addition to aerodynamic requirements, the airfoil must also meet strength requirements, which affect the required profile thickness at the root of the blades, where the stresses from centrifugal forces and bending are highest. Figure 4 shows typical blade root profiles and their cross-section.

4: Profile cross-sections at root of blades

(a) profile common in radial stages or axial stages with very little camber; (b) thin profile with little camber of flow common in hydraulic machines or turbocompressors (camber line is circle); (c) profile of lightly loaded heat turbine blades (camber line is circle and straight line); (d) profile of heavily loaded heat turbine blade (camber line is parabola); (e) profile of wind turbine blade (NACA 63-209); (f) Cavalieri formula for recalculating profile cross-section for different chord lengths. A [mm²] actual blade profile cross-section; A_Λ [mm²] blade profile cross-section at c_Λ chord length (numbers for profiles in this figure are for 1 mm chord length, the so-called specific profile cross-section).

Density of profile cascade

Number of blades

The required camber of flow is a function of the camber, of pitch, of chord respectively the number of blades, where the ratio between the length of the chord and the pitch of the profile cascade is referred to as a density of profile cascade, see Formula 6.

6: Density of profile cascade

σ [1] density of profile cascade.

Diffuser cascades

Confuser cascades

Mean width of blade passage

Pfleiderer, 2005

With a higher density of the profile cascade, a greater camber of flow can be expected and vice versa. On the other hand, the number of blades and frictional losses in the cascade increase with the density of the profile cascade. Thus, there is an optimum value for the density of the profile cascade. In the case of diffuser profile cascades, the optimum density should be sought to be one at which the c/a_m ratio is around 2,5, where a_m is the mean width of blade passage [Pfleiderer and Petermann, 2005, p. 408], see Formula 7. These ratios are valid for profile cascades composed of thin, low camber profiles.

7: Estimation of optimal density of profile cascade

a_m [m] mean width of blade passage. The derivation of the equation is shown in Appendix 5.

Zweifel coefficient

Japikse, 1997

The density of profile cascade with highly camber heat turbine profiles can be approximated by the Zweifel coefficient. The Zweifel coefficient C_L,θ is the ratio of the tangential component of the force on the blade from the fluid flow F_θ to the product of the blade area and the dynamic pressure of the relative velocity at the outlet of the blade cascade, see Formula 8. The value of this coefficient for the designed profile cascade should be in the range of 0,75...0,85 for modern profiles with high blade material strength up to 1 [Japikse, 1997, p. 6-17].

Radial stage

Angles of camber line

Francis turbine

The properties of the radial stages depend significantly on the angle of the camber line of the profile on the rotor circumference (Figure 9), see dimensionless characteristics of radial stages. However, the best aerodynamic properties have backward curved blades whose camber line corresponds to a logarithmic spiral, see Problem 1. In the case of turbine radial stages, the angle of the camber line of the profile at the rotor circumference other than 90° is practically only found in Francis turbines.

9: Effect of camber line angle of profile on blade shape of radial stages of working machines

(a) backward curved blades; (b) radial blades; (c) forward curved blades.

Shapes of blades

The shape of the blade can be either straight, i.e. it is a blade with the same profile along its length, or twisted, where the shape of the profile and the stagger angle of the profile changes along the length of the blade. Apart from these two basic shapes, we can also talk about the blade shapes of radial stages.

Straight blades

Straight blades of axial stages are usually used where a small ratio between blade length and mean blade radius can be achieved, so that the spatial character of the flow is not so apparent. The advantage of straight blades is the simplicity of design, manufacture and cost. They are often manufactured by drawing as circular wires, see Figure 10.

11: Untwisting of twisted blade

(a) illustration of direction of twisting of twisted blade by centrifugal forces; (b) twisted blade with integrated vibration snubber.

Radial blades

Shroud disc

The blades of radial stages are either of such shape that they form purely radial blade passages, or such that they extend into the axial direction (Figure 12(b, c)). In the case of purely radial blades, they are usually straight blades of often constant width, sometimes made of sheet metal (see Problem 3).

12: Examples of radial blade designs for working machines

(a) purely radial blades; (b), (c) radial-axial blades (in case of (c) blades are equipped with shroud disc to reduce internal leakage). The index _t indicates the tip of the blade, _h the root of the blade or the radius of the shaft. r_m [m] mean radius of blade; ε [°] inclination of streamline with respect to axis of rotation.

Inducer

Cavitation

The axial part of radial blades is used in turbine stages and working machines. In turbines, it has the function of uniformly transferring flow from radial to axial direction with a reduction of tangential velocity component V_2θ. The axial part is called the inducer in the case of working machine stages. In pumps, the inducer is usually not pronounced (Figure 12c) to avoid large differences between velocities at the root and tip of the inducer blades, which could cause cavitation. The axial part of the radial rotor is calculated at three radii, i.e., in addition to the middle one, at the tip and at the root of the blade, so that the angle of attack for working machines or the angle of deviation for turbines is constant over the height of the blade (see 2D-calculation of inducer). The manufacture of this part of the blade by machining is difficult and therefore this type of rotor consists of several parts - see Figure 13.

Spiral casings

The basic design of the spiral casing is based on the theory of potential flow, in which the streamlines have the shape of logarithmic spiral. The basic spiral casings shapes are shown in Figure 14, with some shapes not satisfying the conditions of the potential flow equations, resulting in vortices. However, they have other advantages - in particular, they reduce the required diameter of the spiral casing, which results in a much larger diameter than the rotor diameter for a constant casing width and potential flow. Spiral casings can also be reduced by ending them at less than 360°, see Problem 4 - shortened casings can be used where size is a more important parameter than efficiency.

14: Basic spiral casings

(a) rectangular (constant casing width - mainly used in fans); (b) trapezoidal (gradual extension leads to lower losses than step extension and its shape is very close to the condition for potential flow); (c) circular; (d) tangential outlet casing. b [m] casing width.

Axial branches

Side branches

Jet engine

Mattingly et al., 2002

Figure 15 shows some designs of axial and side branches. In the case of Figure 15b, the jet engine axial beveled branch that allows for more optimal pressure distribution of the first stage of compressor. The maximum engine power (air consumption) is during takeoff, and therefore the angle α approximately corresponds to the pitch angle during takeoff. More details on this issue, including the calculation of the optimal deflection angle α, are given in [Mattingly et al., 2002, p. 424].

15: Branches of axial stages

(a) axial inlet (e.g. combustion turbine inlet); (b) jet engine inlet; (c) axial outlet (e.g. axial fan outlet); (d) side branches (e.g. axial compressor side branches). α [°] deflection angle.

(a) rotor; (b) stagger angle detail; (c) manufacturing drawing of blade. ω [°] auxiliary angle.

References