AERODYNAMICS OF PROFILE CASCADES

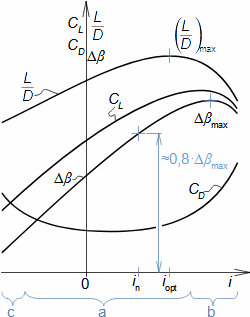
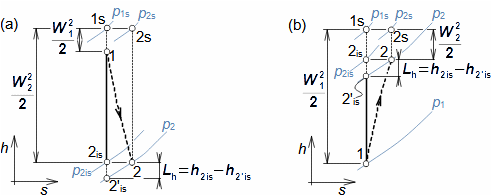
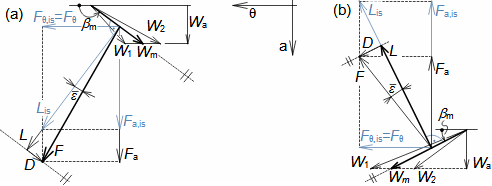
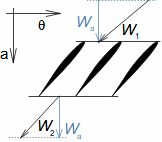
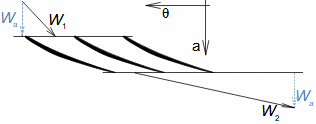
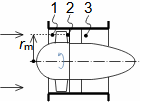
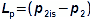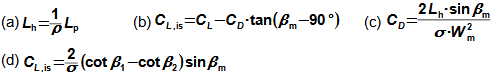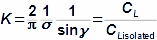Basic concepts of aerodynamics of profile cascades

Airfoil aerodynamics

Drag

Lift

The aerodynamics of profile cascades is based on the definitions of aerodynamic quantities used in the description of the airfoils aerodynamics [Škorpík, 2022, Aerodynamics of airfoils]. This means that for a profile included in a profile cascade, one can also distinguish between drag and lift, which can be calculated using the same formulas as in the case of airfoils, with the difference that instead of the attack velocity, the mean aerodynamic velocity in the cascade is assumed, so that the drag is in the direction of this mean velocity and the lift is perpendicular to this velocity, see Formulas 1.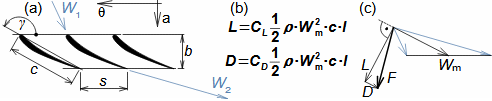

1: Formulas for blade drag and lift in blade cascade

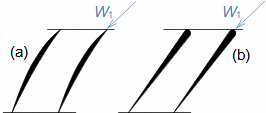
(b) section through linear blade cascade; (b) formulas for calculating drag and lift of straight blade in linear blade cascade; (c) relations between velocities and forces acting on straight blade. D [N] drag; L [N] lift; F [N] force on blade; ρ [kg·m^-3] working fluid density; W_m [m·s^-1] mean aerodynamic velocity in cascade; c [m] chord; γ [°] stagger angle of profile in cascade; b [m] width of blade cascade; l [m] length of straight blade; C_D, C_L [1] drag and lift coefficient of profile in profile cascade; s [m] pitch. θ, a-labelling of axes in coordinate system.

Lift coefficient

Drag coefficient

Wind tunnel

Japikse,1997

The aerodynamic coefficients C of the profiles in the cascades are measured in the wind tunnels of the linear blade cascades (Figure 2) for different combinations of velocities and angles of attack. The blade cascade in the wind tunnel consists of several (5 to 7) straight blades inserted obliquely into the tunnel so that the working fluid flow follows the direction of relative velocity in the actual blade cascade. The inlet and outlet flow areas of the tunnel correspond to the flow areas of the blade cascade under test. Wind tunnel designs for compressor blade cascade are given, for example, in [Japikse, 1997, p. 11-7] and for turbine blade cascades in [Japikse, 1997, p. 6-22].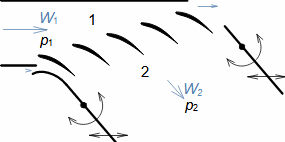

2: Wind tunnel for measuring blade cascades

Blade passage

Howell, A. R.

Carter, A. D. S.

Lieblein, S.

Japikse,1997

Dixon and Hall, 2010

The blade passages in turbomachines change their shape and size along their length as the profile and pitch of the blades that define these passages change. Especially for twisted blades, there are large changes not only in the geometric but also in the aerodynamic parameters of the flow, so that a large number of measurements are necessary for aerodynamic calculations. Measurement of aerodynamic quantities for a combination of so many variables is time and costly and therefore computational methods have been developed to predict the change in aerodynamic quantities of profiles when some parameters are changed, e.g. Howel's, Carter's, Lieblein's...[Japikse, 1997, p. 5-14], [Dixon and Hall, 2010]. These methods are particularly useful when trying to reduce the amount of measurements needed for small changes on the profile and profile cascade.

Pressure loss of profile cascade

Pressure loss, which is mainly due to internal friction of the working fluid, can be indicated when flowing through any channel. In the case of blade passages, respectively blade cascade, the pressure loss L_p is defined as the difference by which the pressure behind the cascade p₂ must be reduced so that the velocity behind the cascade W₂ is the same as the velocity W_2is when flowing through the cascade without losses at the outlet pressure p_2is, see Equation 4. The condition in front of the cascade is assumed to be the same for both cases.

4: Pressure loss of profile cascade

L_p [Pa] pressure loss; p_2is [Pa] pressure behind cascade at flow without losses; p₂ [Pa] pressure behind cascade when same velocity are reached in front of and behind cascade W_{1, 2}.

Profile loss of profile cascade

Profile losses of the profile cascade are the undesired energy transformations (energy dissipation) in the working fluid that occur during the flow through the profile cascade. Profile losses include, in particular, internal friction losses, flow separation losses from the profile, vortex loss behind trailing edge and shock wave losses at high flow velocities. The sum of these losses gives the profile loss of the cascade.

Vortexing

Trailing edge

The trailing edges of blades are not sharp mainly for strength reasons, so there is a gap between the flows from the suction and pressure sides of the blades in which small vortexes are formed due to the different velocities of these flows, see Figure 6.

6: Vortexing behind trailing edge

Shock wave

Critical Mach number

The velocity of the flow varies along the profile, so that even if the flow does not reach the speed of sound before the cascade, it can reach or even overcome that speed at a certain attack velocity in the cascade, which we refer to as the critical Mach number of the profile cascade. When the velocity subsequently drops back to subsonic, a shock wave can, under certain conditions, be generated. Details of high velocity flow in profile cascades are given in the chapter Aerodynamics of profile cascades in compressible flow in [Škorpík, 2023c].

Energy balance

The profile loss of the blade cascade is equivalent to the enthalpy by which the isentropic enthalpy difference behind the cascade must be reduced in order for the outlet velocity to be the same as in the case of a lossless flow, see Figure 7.

7: Energy balance of blade cascade profile losses

(a) situation in confuser cascade; (b) situation in diffuser cascade. h [J·kg^-1] enthalpy; s [J·kg^-1·K^-1] entropy; p_s [Pa] stagnation pressure; L_h [J·kg^-1] profile losses. The index _is denotes the change of state in lossless flow.

Lift coefficient

Drag coefficient

Profile loss

Pressure loss

The equations for calculating the lift and drag coefficient and the profile loss of the profile cascade (Equation 10) can be derived from the previous figure and the pressure loss. These equations can also be used in reverse to calculate the pressure loss based on aerodynamic quantities. Taking Equation 10d for the lift coefficient for the lossless flow case C_L,is is derived from the camber of flow requirement and Equation 10b is derived from the actual values of the aerodynamic coefficients-the right sides of these equations are equal for a well-designed profile cascades.

10: Equations for calculation of aerodynamic quantities of profile cascades

C_L,is [1] lift coefficient for the case of flow without profile losses; σ [1] density of profile cascade. The orientation of the attack and outflow velocity angles β₁, β₂ is the same as the orientation of the angles β_m in Figure 9. The derivation of the equations is shown in Appendix 5.

Transferability of linear blade cascade aerodynamics to aerodynamics of diagonal and radial blade cascades

Transformation equations

Nožička, 1967

Japikse,1997

In Problem 2, the application of aerodynamic data obtained from measurements on a linear blade cascade to the axial blade cascade is demonstrated, but these data can also be applied to radial and diagonal blade cascades. In this case, the blade shape of the non-linear cascades must be transformed point by point to the linear cascades. Figure 11 shows an example of transforming the shape of a circular blade cascade to a linear cascade using the transformation equations. A diagonal blade cascade can be transformed in a similar way [Nožička, 1967, p. 84], [Japikse, 1997, p. 7-24]]. Similarly, the pressure and velocity fields measured on a linear blade cascade must be transformed back into circular coordinates by the procedure derived in [Nožička, 1967, p. 84]. These transformation equations are derived under the simplifying assumption of potential flow.

12: Weining coefficient

C_Lisolated [1] lift coefficient of isolated plate. The formula has validity up to approximately 1/σ= 0,7, from which value the graph given in [Lakshminarayana, 1996, p. 212] can be used. From a value of 1/σ=2,5, the K factor is close to 1.

Wind turbines

Propellers

Besides the Weinig coefficient, there are other ways to determine the lift coefficient of a profile in a cascade if its parameters are known when measured as an airfoils. These methods are used in the calculation of blade cascades of wind turbines and propellers, more in the article Aerodynamics of wind turbines.

Drag coefficient

If the flow separation from the airfoil does not occur, the drag coefficient of the airfoil C_D in an cascade can be expected to be less sensitive to aerodynamic interference than the lift coefficient C_D. Thus, the aerodynamic calculation of a profile cascade designed in this way can be started by using the values of the lift coefficient and the profile drag to calculate the lift coefficient C_L,is etc., according to Equation 10 for the lift coefficient C_L and the proposed angle of mean aerodynamic velocity β_m, see Problem 4.

Base airfoil

In the case of profiles with a camber of a base airfoil (usually profiles with a camber greater than that of airfoils), the calculation of the forces on the blade can be based on the properties of the original base airfoil. The calculation is based on the assumption that the drag coefficient C_D of the profile does not change much after cambering, so other force values can be determined based on the calculation of the profile drag in the cascade D as shown in Figure 9.

Problems

r_m [m] mean radius of blades.

References