INTERNAL LOSSES OF TURBOMACHINES AND THEIR INFLUENCE ON TURBOMACHINE DESIGN

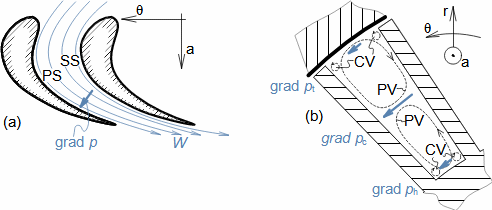
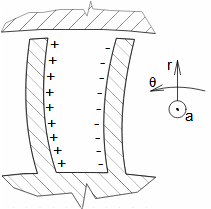
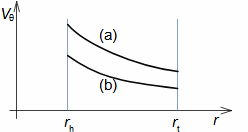
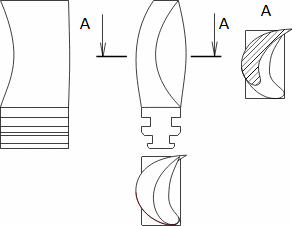
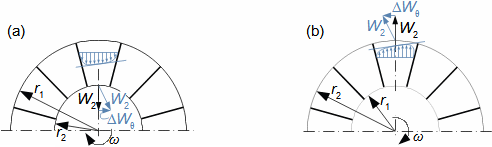
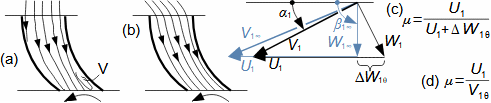
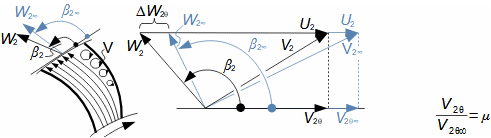
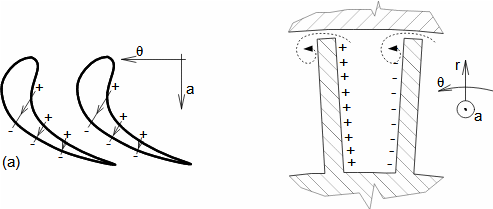
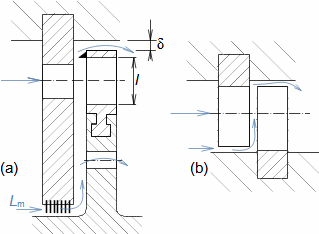
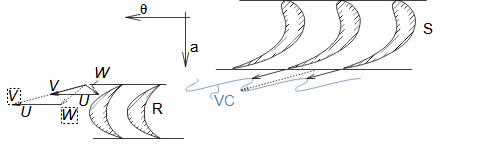
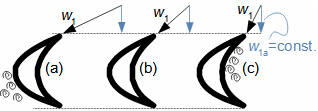
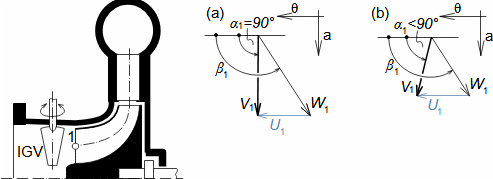
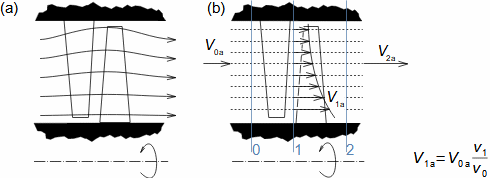
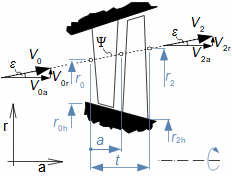
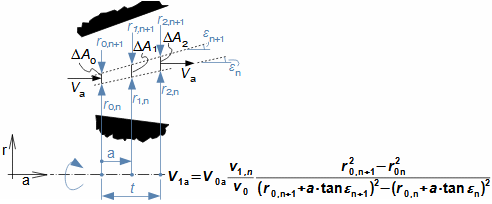
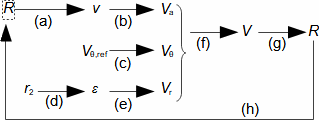
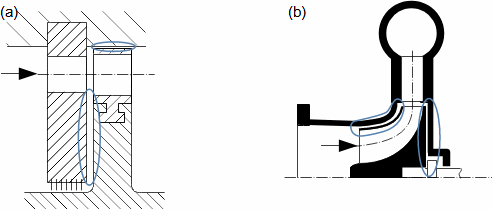
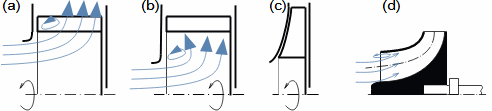
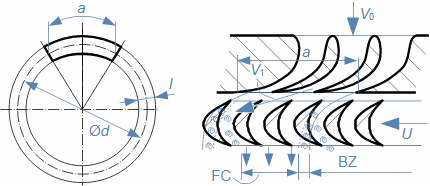
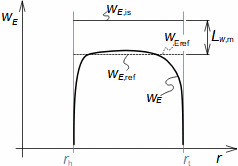
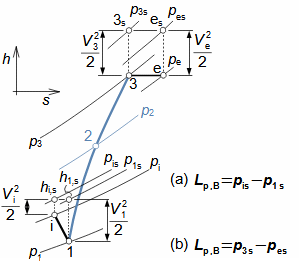
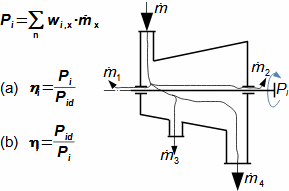
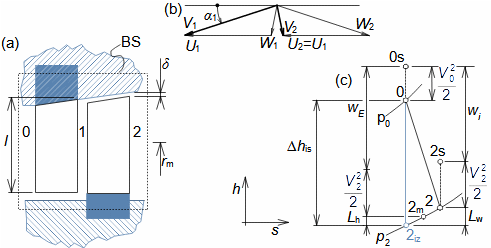
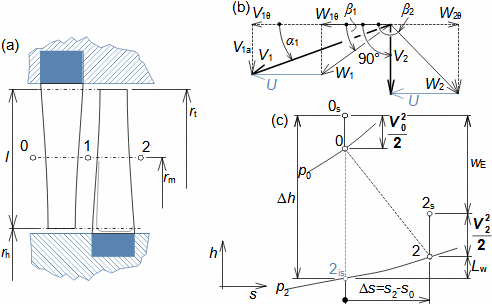
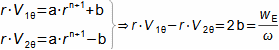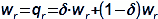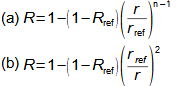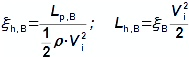Essential concepts for description of internal losses in turbomachines

The internal losses L_w as the difference between the ideal work and the actual work of the machine are always caused by some transformation or transfer of energy in the individual parts of the machine with different intensity. Apart from profile losses, other types of internal losses also occur, for example, through leakages, friction between the working fluid and the casing and shaft, etc. The individual types of losses are defined in such a way that they can be added together in the final energy balance of the machine to give the final value of internal losses according to Formula 1. However, many types of losses interact to a greater or lesser degree and this must be taken into account in the final calculation. The calculation of internal losses is done within a single stage (internal stage losses) or the whole machine internal machine losses, etc.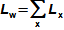

1: Internal losses

L_w [J·kg^-1] internal losses in machine part under investigation; L_x [J·kg^-1] value of individual loss in machine part under investigation. x-identification of investigated type of loss.

Loss coefficient

The ratio of the individual loss to the ideal work is the loss coefficient (Formula 2a), but depending on the type of machine, the losses and the practices in the field, it can also be defined to the internal work (Formula 2b) or other process.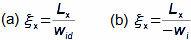

2: Loss coefficient

ξ_x [1] loss coefficient of individual loss; w_id [J·kg^-1] ideal work of working fluid; w_i [J·kg^-1] internal work of working fluid.

Calculation of losses

Ideal process

The calculation of losses is conditioned by the knowledge of the dimensions and parameters of the machine part under investigation and the definition of the ideal process (state). This means that the determination of losses is iterative. For example, by initially designing the machine or part of the machine for the case of no loss flow or with only loss estimates, and only after this design is the actual losses calculated and any changes in dimensions and parameters performed to reduce losses, etc. The calculation is most often based on semi-empirical relationships developed for the machine type, numerical calculations (modelling) or on the designer's ability to use his/her broad knowledge of the behaviour of similar machines/stages to predict the loss for a new yet unresolved case.

Angle of attack

Mach number

Dixon and Hall, 2010

The value of the secondary flow loss increases, for example, with increasing angle of attack and decreasing Mach number. A prediction of the changes in velocity angles due to secondary flow for twisted blades is made, for example, in [Dixon and Hall, 2010, p. 212].

Bowed-twisted blade

Sloping blade

Japikse, 1997

To reduce the secondary flow loss of axial stages, sloping the blades away from the radial axis is done, but more effective is blowed them (Figure 4) [Japikse, 1997, p. 6-13].

4: Bowed-twisted blade (3D stacks)

Bowed-twisted blade

Axial stage

Euler work

The shape of the Bowed-twisted blade of the axial stage is not designed under the condition of constant circulation of the tangential velocity component (the condition of the irrotational vortex), but on the contrary under the condition of its change according to some exponential function. For example, according to the function defined by Equation 5, see Figure 6. This equation is advantageous in that the Euler work along the length of the blades is constant as in the case of potential flow (the irrotational vortex equation is a special case of this equation).

5: Axial stage equations with constant Euler work and exponential velocity circulation

V [m·s^-1] absolute velocity; r [m] radius; w_E [J·kg^-1] Euler work on investigated radius; ω [rad·s^-1] angular velocity of rotor rotation; a, n [SI] proposed constants; b [SI] constant (can be calculated from proposed Euler work on reference radius).

8: Opposite circulation in blade passage of radial stage

(a) direction of opposite circulation; (b) centripetal flow; (c) centrifugal flow. Ω [rad·s^-1] angular velocity of opposite circulation; a_r [m·s^-2] centrifugal acceleration; a_c [m·s^-2] Coriolis acceleration.

Radial velocity component

Tangential velocity component

Slip

Opposite circulation causes uneven radial velocity component in the blade passage — accelerating one side, decelerating the other — and the change in the tangential component of the outlet velocity, which is called slip (Figure 9(a, b)). Opposite circulation in effect reduces the value of the Euler work due to the unfavourable change in the tangential component of the velocity W_2θ and hence V_2θ at the rotor outlet.

9: Change in radial and tangential velocity components due to effect of opposite circulation

ΔW_θ [m·s^-1] deviation of tangential component of relative velocity at rotor outlet caused by opposite circulation.

Slip coefficient

Dixon and Hall, 2010

A quantity called the slip coefficient is used to predict the effect of the opposite circulation on the Euler work. The slip is defined separately for the turbine stages (Figure 10) and for the working machine stages (Figure 11).

10: Definition of slip coefficient of radial cetripetal turbine

(a) effect of opposite circulation on flow; (b) in case of centripetal turbines it is possible to compensate slip by changing angle of absolute velocity in front of rotor, thus changing angle of relative velocity; (c) general formula for slip coefficient; (d) special formula for slip coefficient at β_1∞=90° (other cases, for example, in [Dixon and Hall, 2010, p. 279]). μ [1] slip coefficient for centripetal turbines; β [°] relative velocity angle. V-vortices that arise during flow separation from blades. The index _∞ denotes the parameters of the velocity triangle for the case of an infinite number of blades (the case where no opposite circulation arises).

13: Tip leakage losses

(a) leakage in case of impulse stage with disc type rotor and blades with shrouds; (b) loss of internal leakage in case of stage without shrouds. L_m [kg·s^-1] mass flow through stage leaks; δ [m] radial gap length; l [m] blade length.

Disc type rotor

Japikse, 1997

Zekui, 2025

Flow through leaks can disrupt the main flow because it has higher energy. Therefore, in the case of disc type rotors, the leakage of the previous blade cascade is sucked out through a hole in the disc outside the blade passages (Figure 13a). The leakage of blades without shrouds also affects the tip clearance losses, see Problem 1. Formulas for approximate determination of the tip leakage losses are given in [Japikse, 1997, pp. 6-35], [Zekui et. al., 2025] (in Czech [Kadrnožka, 2004, p. 95, 200]).

Misárek, 1963

The loss coefficient of tip leakage loss decreases with the length of the blades, respectively with the ratio of the length of the blades l and the radial gap δ. In addition, for working machine stages, leakage can be positive in some operating conditions because it stabilizes the stage flow. The dependence of the blade length on the efficiency of the compressor stage is given, for example, in [Misárek, 1963, p. 73].

Loss of uneven velocity distribution in front of cascade

Boundary layer

Velocity triangle

There is a uneven velocity distribution at the outlet of the blade cascade, which is caused by friction in the boundary layer of the flow at the blade surfaces on both the suction and pressure sides. This non-uniform velocity contour of the working fluid causes the attack angle and velocity, respectively the velocity triangle, to change alternately as the rotor blade cascade moves through such the velocity field, see Figure 14.

Turnable blades

Rotational speed

Inlet guide vanes

The optimum angle of attack when changing the flow through the stage can be kept by changing the rotational speed. If it is not possible to change the rotational speed, then the angle of attack can be kept within the optimum limits by turnable blades. For single stage axial and radial work machines, inlet guide vanes can also be used, see Figure 16. When the flow rate is changed, the inlet guide vanes are rotated so that the inlet angle of the relative velocity to the rotor cascade is changed as little as possible, thus achieving the least decrease in efficiency due to the change in angle of attack.

16: Regulation of angle of attack into rotor of radial compressor stage by using inlet guide vanes

(a) velocity triangle at leading edge of inducer in case of nominal flow; (b) deflection of absolute velocity from axial direction by inlet guide vanes so that inlet angle β₁ is kept even at reduced flow. IGV-inlet guide vanes. α [°] absolute velocity angle; β [°] relative velocity angle.

Loss through backflow

This type of loss is related to a reduction in the mass flow rate of the stage compared to the nominal state. In the case of reduced flow, significant flow separation from the meridional surfaces of the blade passages (at the foot of the blades) and backflow can occur, as shown in Figure 17.

17: Backflow of long twisted blade when flow through turbine stage is reduced

Losses due to change of meridional velocity

Outlet velocity

Flow area

It is an effort to make the outlet velocity of the turbomachine the same as the inlet velocity. If the outlet velocity is higher, it means the energy of the working fluid was not transformed into internal work, but remained as kinetic energy, which represents a loss. Of course, there are cases where an increase in outlet velocity is desirable (propellers, jet engines, etc.). Changing the meridian velocity can generate other types of losses as well. For example, in heat turbines, the specific volume increases during expansion and not only the outlet velocity but also the profile losses increase for the same flow areas. Similarly, compression in turbocompressors results in a decrease in velocity for the same flow area. That is, frictional losses may decrease, but as velocity decreases, blade camber must be increased (to maintain the same Euler work of stage, or tangential velocity component), which can lead to flow separation from the blades.

Normal stage

Twisted blade

For heat turbines and turbocompressors, it is therefore necessary to gradually change the flow areas so that the inlet and outlet velocities of the stage remain approximately the same. Stages with this condition are also called normal stages. While for radial stages the changes in the inlet and outlet flow areas do not have a significant effect on the stage design procedure, for axial stages the design intervention is much more significant because the radial component of the velocity must also be considered as the blade lengths change - hence the term conical stage, see Figure 19.

19: Examples of cone stage performances

ε [°] angle between axial direction and direction along conical surface. Further examples of conical stages are shown in the article Thermodynamics of heat turbines.

Reaction

Reaction R for each radius must be calculated iteratively. First, an estimate of the reaction for the radius under investigation is made and from this the working gas parameters are determined, from which the velocities and reaction are then calculated and the value of reaction is compared with the estimate, see Figure 22.

22: Iterative calculation of reaction of axial stage

R [1] reaction. (a) estimate reaction R and from h-s diagram or by calculation determine specific volume at outlet of first blade cascade; (b) calculate axial velocity component; (c) calculate tangential velocity component from constant velocity circulation formula and given triangle on reference radius; (d) calculation of outlet radius of stage according to Formula 20 and angle ε; (e) calculation of radial component of velocity; (f) calculation of absolute velocity; (g) calculation of reaction from velocities; (h) comparison with original estimate of reaction, if the accuracy of the estimate was not sufficient, then calculation is repeated with new estimate. The index _ref denotes the entered parameters at the reference radius.

Kadrnožka, 2004

Pfleiderer and Petermann, 2005

The above procedure for designing a conical stage is only one of many possible variations; for example, in [Kadrnožka, 2004], [Pfleiderer and Petermann, 2005] the slope of the conical surfaces is prescribed and then the inlet and outlet velocities of the stage are iteratively calculated at individual radii.

Rotor friction loss

Rotor

Euler work

Friction

Disc type rotor

Radial stage

Shroud

Rotor friction loss is equivalent to the portion of Euler work that must be expended to overcome the frictional resistance of the working fluid against the rotation of the rotor - so the mean value of Euler work must be greater than the internal work of the stage. Significant rotor friction losses arise, for example, in disc type rotor (Figure 23a) where there is a relatively large disc area in contact with the working fluid enclosed between the disc and the stator. It is also significant in radial stages (Figure 23b). Rotor friction loss also occurs at the bounding surfaces between the rotor and stator (shroud), but this loss is relatively small.

Misárek, 1963

Extensive information from measurements of the effect of different types of losses on the efficiency of the radial compressor stage is shown in [Misárek, 1963].

Loss due to partial admission

Flow separation

Friction

Kadrnožka, 2004

Loss due to partial admission occurs in cases where fluid flows into the stage on only part of the circumference of the rotor blade cascade, see Figure 26. The loss is realized in the marginal zones (swirling of the fluid due to the flow separation from the blades) and by friction of the blades against the stationary working fluid outside the working area. Details on the mechanism of loss due to partial admission and its approximate calculation are shown in [Kadrnožka, 2004, p. 196].

26: Partial admission rotor blade cascade

a [m] length of stator blade cascade (nozzle group); l [m] length of blades; FC-flow core; BZ-border zone.

Laval turbine

Nozzle governing

Combustion turbine

Loss due to partial admission occurs in single-stage turbines, e.g. Laval turbines (where the stator cascade of blades does not cover the entire circumference) or in nozzle governing steam turbines and also in combustion turbines with tube combustion chambers.

Example of procedure to design stage with losses

Model

When deciding on the design procedure for a turbomachine stage, the requirements for its power parameters, price, cost of operation, method of operation and whether it is a machine for series production or piece production are taken into account. For this reason, a universal procedure for calculating turbomachine losses cannot be described. The design of the flow parts of turbomachines can generally be said to be designed according to analytical calculation models and their parameters can be optimised and refined using computer calculation models.

28: Reaction of axial stage with constant Euler work and incompressible fluid

(a) reaction for case of tangential velocity component proposal according to Formula 5; (b) reaction for case of tangential velocity component proposal according to equation for irrotational vortex (n=-1). The index _ref denotes the quantity at the reference radius of the blade. The derivation is shown in Appendix 5.

Losses in turbomachine branches

The branches must keep the fluid pressure uniform around the entire circumference of the inlet part of the first stage and the outlet part of the last stage of the machine. In the inlet branches, the working fluid is usually slightly accelerated towards the first stage. In the outlet branches, the working fluid is usually slightly decelerated towards the last stage. In both cases, the change in velocity compensates for the pressure loss. The loss in the branch is usually related to the kinetic energy of the fluid in front of the branch, see Formula 29.

29: Loss coefficient and specific loss in branch

L_h,B [J·kg^-1] branche loss; V_i [m·s^-1] mean velocity in branche inlet section; L_p [Pa] branche pressure loss; ρ [kg·m^-3] density; ξ_B [1] loss coefficient of branche.

h-s chart of branche

Figure 30 shows the h-s chart of the thermodynamic changes occurring in the branches of a working machine. The pressure in the inlet branche gradually decreases as the flow area reduces (suction takes place here). Approximately throttling occurs in the outlet branche to compensate for the branche pressure loss (total pressure decreases), or there is a slight compression to stabilize the boundary layer. Especially for fans, there is a direct diffuser behind the outlet branch, in which part of the kinetic energy of the gas is transformed into pressure energy.

Problems

(a) meridional section of stage; (b) velocity triangle on mean radius; (c) h-s diagram of stage. η_E [1] Euler work efficiency; l [mm] blade length; α [°] absolute velocity angle; W [m·s^-1] relative velocity; h [J·kg^-1] enthalpy; s [J·kg^-1·K^-1] entropy; L_h [kJ·kg^-1] profile losses at mean radius; L_w [kJ·kg^-1] internal losses; Δh_is [kJ·kg^-1] isentropic change of enthalpy; m [kg·s^-1] mass flow. The index _m denotes the mean radius of the blades.