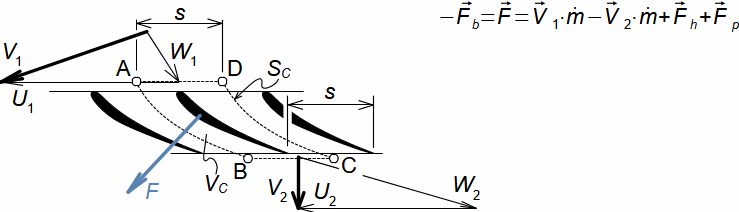
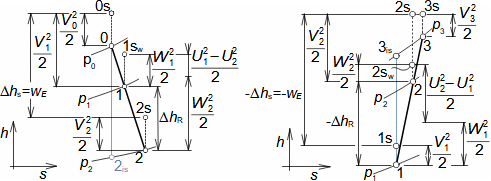
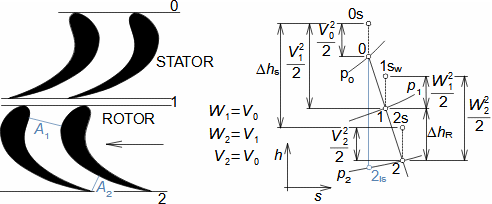
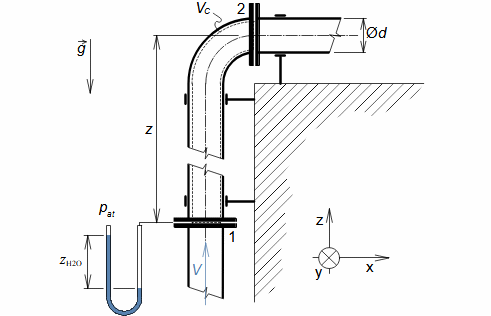
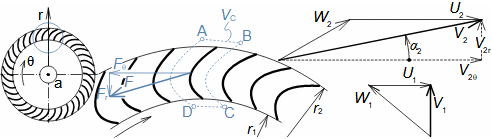
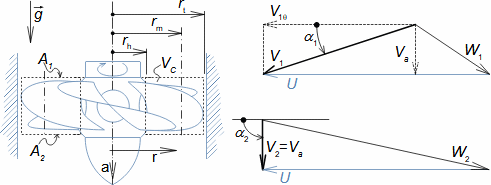
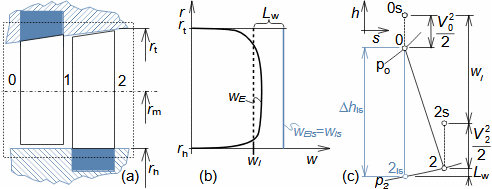
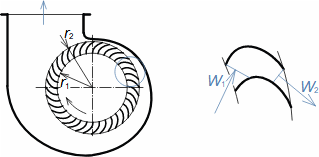
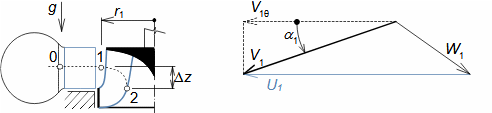
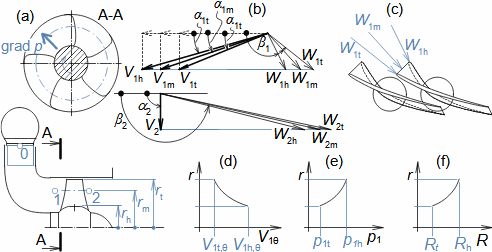
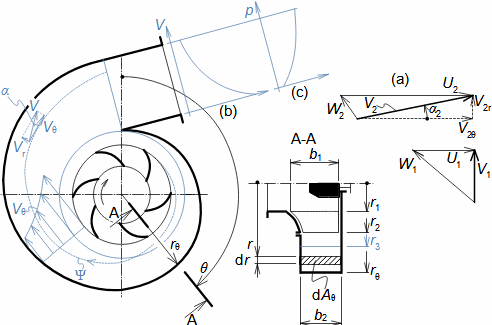
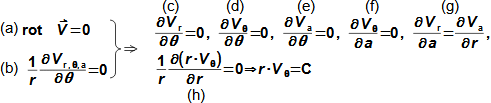turbomachinery.education 
2.

ESSENTIAL EQUATIONS OF TURBOMACHINES

2.3 . . . . . . . . . . . . . .
Equation for calculating forces acting on machine surfaces from fluid flow
Theorem of momentum change – Force on blade
2.5 . . . . . . . . . . . . . .
Equations for calculating energy distribution in turbomachine stage
Euler work – Reaction
2.8 . . . . . . . . . . . . . .
Equations for calculating velocity distribution at ideal flow in turbomachine
Equation of axisymmetric potential flow - Euler equation of hydrodynamics
2.10 . . . . . . . . . . . . . .
Problem 1: Calculation of forces on pipe from fluid flow
Problem 2: Calculation of force on fan blade
Problem 3: Calculation of force on water turbine blade
Problem 4: Calculation of Euler work in turbomachine stage
Problem 5: Calculation of reaction of steam turbine
Problem 6: Calculation of reaction of fan
Problem 7: Calculation of reaction of Francis turbine
Problem 8: Velocity and pressure distribution in Kaplan turbine
Problem 9: Calculation of logarithmic spiral and spiral casing dimensions
Problem 10: Calculation of dimensions of bladeless stator
2.15 . . . . . . . . . . . . . .
References
2.16 - 2.33 . . . . . . . . .
Appendices
View PDF
turbomachinery.education  
2.2
author:
ŠKORPÍK, Jiří – LinkedIn.com/in/jiri-skorpik
issue date:           
September 2009; September 2022 (2nd ed.)
title:
Essential equations of turbomachines
proceedings:
turbomachinery.education
provenance:
Brno (Czech Republic)
email:
skorpik.jiri@email.cz

Copyright©Jiří Škorpík, 2016-2022
All rights reserved.

KeywordsChapter: Equation for calculating forces acting on machine surfaces from fluid flow
2.3

Equation for calculating forces acting on machine surfaces from fluid flow

The forces acting from a fluid flow on a machine surfaces can be determined from the momentum change theorem. Its special form is also used to calculate the forces acting on a blades in a blade cascade from a fluid flow, a classical problem in turbomachinery.

Theorem of momentum change

Control volume

Pressure forces

Weight

Force from bodies

Forces acting from a fluid flow on machine surfaces can be determined from the momentum change theorem (Newton's second law). According to the momentum change theorem, a change in fluid momentum over time is equal to the sum of the external forces acting on the fluid in the control volume. In the case of applying this law to a fluid enclosed in a control volume VC (Figure 1), the external forces considered are: the pressure forces from the surrounding fluid at the boundaries of the control volume Fp, the weight of the fluid in the control volume Fh, and the forces exerted by the bodies inside and at the boundaries of the control volume Fb. The change in momentum of the fluid inside the control volume is also equal to the difference of the product of velocity and mass flow between the inlet and outlet of the control volume.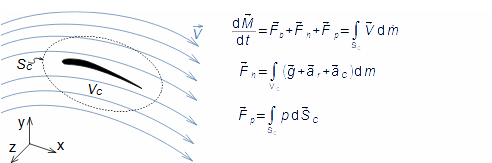

Theorem of momentum change
1: Theorem of momentum change
VC [m3] control volume; SC [m2] surface of control volume boundary; V [m·s-1] velocity of working fluid; M [N·s] momentum of fluid inside control volume; t [s] time; Fb [N] resultant of forces acting on working fluid from bodies inside and on control volume boundary; Fh [N] weight of working fluid inside control volume; Fp [N] forces from pressure of surrounding fluid on surface of control volume; m• [kg·s-1] mass flow; g [m·s-2] gravitational acceleration; ar [m·s-2] centrifugal acceleration; aC [m·s-2] Coriolis acceleration; p [Pa] pressure; m [kg] mass. The derivation of these equations assuming steady fluid flow through the control volume is shown in Appendix 11.
KeywordsChapter: Equation for calculating forces acting on machine surfaces from fluid flow
2.4

Force on blade

Control volume

Relative velocity

Pitch of blades

Velocity triangle

When calculating turbomachine blade forces, define control volume boundaries where parameters for momentum change theorem are known. Therefore, the control volume in Figure 2 is defined to pass through the center of the blade passage, or the boundaries AD and BC are spaced apart by the pitch of blades. The boundaries AD and BC are the expected streamlines of the relative velocities W of the velocity triangle of this blade cascade. The blade passages are equal in a single blade cascade, so that the action of the pressure forces at the AD boundaries cancel with the action of the pressure forces at the BC boundaries. The integration of the product of the absolute velocity V and the mass flow is also cancelled at these boundaries, see Equation 2.

Force on blade from fluid flow
2: Force on blade from fluid flow
Both velocities and forces are vector quantities, but the arrow above the velocity symbols in the velocity triangle is usually not shown. F [N] resultant of forces acting on blade; W [m·s-1] relative velocity; U [m·s-1] blade speed; m• [kg·s-1] amount of working fluid flowing through control volume; s [m] pitch of blade. The derivation of this equation for the assumption of stationary flow through the control volume is shown in Appendix 12.

Cylindrical coordinate system

Radial force

Tangential force

Axial force

Thrust bearing

Typical for the investigation of forces in a turbomachine stage is the use of cylindrical coordinate system. The force F in the cylindrical coordinate system has three spatial components, namely a component in the radial direction Fr, in the tangential direction Fθ (this force produces torque) and in the axial direction Fa (it causes stress on the rotor in the axial direction and is collected by a thrust bearing) - these force components are abbreviated as radial, tangential and axial forces.

Mean aerodynamic velocity

The force acting on the blade is approximately perpendicular to the mean aerodynamic velocity in the blade cascade Wm, which is the mean of the relative velocities at the inlet W1 and outlet W2. Respectively, it can be shown (see Equation 3) that the resulting force on the blade from the incompressible fluid flow F is perpendicular to the mean aerodynamic velocity Wm in lossless flow.

KeywordsChapter: Equation for calculating forces acting on machine surfaces from fluid flow
2.5
Definition of mean aerodynamic velocity in blade cascade and its relation to force vector acting on elementary blade (blade length dr)
3: Definition of mean aerodynamic velocity in blade cascade and its relation to force vector acting on elementary blade (blade length dr)
Wm [m·s-1] mean aerodynamic velocity in blade cascade; βm [°] angle of mean aerodynamic velocity; ε [°] angle of resultant force. This equation is derived for the elementary blade length Δr and the axial blade cascade in Appendix 13 and its validity is limited to incompressible flow without losses (isoentropic - index is).

Equations for calculating energy distribution in turbomachine stage

Meridional direction

The proposal of the energy distribution or transformation in the turbomachine stage is based on two directions. In the direction perpendicular to the meridional direction, an Euler work distribution, which is the local value of the internal work, is proposed. In the meridional direction, the proposal of the reaction, which describes the distribution of energy transformations between the stator and the rotor of the stage, decides the characteristics of the stage.

Euler work

Internal work

Losses

Euler turbomachinery equation

The Euler work is the fluid work transferred to the blades in the surroundings of the streamline under investigation, see Figure 4(b). The difference with the internal work of the stage wi is that the internal work of the stage is the mean work of all the working fluid flowing through the stage (including gaps) and can be determined from the complete energy balance of the stage, see Figure 4(a). So some of the fluid will do more Euler work than others, but their mean is wi. For actual stages, the largest Euler work is in the core of the flow (at the mean diameter of the blades), where the losses are smallest. Conversely, at the edges of the blades, or near their roots and tips, the Euler work is smallest due to high frictional losses and internal leakage. The Euler work can be determined from the velocity triangles on the streamline under investigation, see Equation 4(c) - Euler turbomachinery equation.

KeywordsChapter: Equations for calculating energy distribution in turbomachine stage
2.6
Difference between Euler work and internal work of stage
4: Difference between Euler work and internal work of stage
wi [J·kg-1] internal work of stage; wE [J·kg-1] Euler work in surroundings of investigated streamline; q [J·kg-1] shared heat with surroundings; ω [°] angular speed. BST-stage boundary; S-stator blade cascade; R-rotor blade cascade, ψ-streamline. The derivation of the Euler turbomachinery equation for the assumption of stationary flow and no weight effect is shown in Appendix 14.

Euler efficiency

Internal efficiency

Similarly, the stage efficiency can be determined in two ways, either to the Euler work (Euler efficiency) or to the internal work (internal stage efficiency), as done in Problem 4.

Reaction

Stator

Rotor

Hydraulic machine

A reaction is the ratio between the change in the static enthalpy in the rotor blade cascade and the change in the stagnation enthalpy of the stage (Formula 5), or the change in the static enthalpy of the stage - depending on convention. Thus, it describes the distribution of the energy transformation between the stator and rotor blade cascades of the stage.

Definition of reaction
5: Definition of reaction
KeywordsChapter: Equations for calculating energy distribution in turbomachine stage
2.7
(a) definition of reaction; (b) simplified reaction formula for hydraulic machines, where approximate equality of enthalpy and pressure energy changes can be assumed (Δh≈Δp·ρ-1). Δhs [J·kg-1] difference between stagnation enthalpy at inlet to stage and outlet from stage; ΔhR [J·kg-1] difference between static enthalpy at inlet to rotor blade cascade and outlet from rotor blade cascade; Δps [Pa] difference between stagnation pressure at inlet to stage and outlet from stage; ΔpR [Pa] difference between pressure at inlet to rotor blade cascade and outlet from rotor blade cascade; ρ [kg·m-3] density.

h-s chart

Stage of turbomachine

A reaction is determined to a specific streamline (radius) similar to Euler work. To calculate the reaction, it is important to know the construction of the h-s chart, from which the differences in specific enthalpies Δhs and ΔhR can be determined (see Problem 5, Problem 6). h-s charts and a description of their construction are showen in Figure 6. In the case of hydraulic machines, the required pressure differences Δps and ΔpR can also be determined from Bernoulli equation for relative flow, see Problem 7 and Problem 6.

h-s charts of turbomachine stages
6: h-s charts of turbomachine stages
left-turbine stages; right-working machine stages. These h-s charts are constructed under the assumption of adiabatic flow without gravity effect. 1sw, 2sw denote the overall condition with respect to the relative motion at the rotor inlet and outlet. A detailed description of the construction of the h-s charts is shown in Appendix 15.

Mean radius

Absolute velocity

Relative velocity

Losses

Most stages are designed with a variable reaction over the length of the blades, while a common requirement in stage design is the reaction at the mean radius of about 0,5 (even a little higher for radial stages due to the difference in blade speeds on the rotor), since at maximum Euler work the absolute velocities in the stator passages are about the same as the relative velocities in the rotor passages, and hence the distribution of losses between stator and rotor is uniform, see Figure 7.

KeywordsChapter: Equations for calculating energy distribution in turbomachine stage
2.8
Example of turbine axial stage blade passages with reaction of 0,5
7: Example of turbine axial stage blade passages with reaction of 0,5
With the same enthalpy differences between the stator and rotor, the velocity triangles are symmetrical and the shape of the blade passages (A1≠A2) is also symmetrical. 1sw is denoted relative stagnation state of working fluid at rotor inlet.

Laval turbine

Pelton turbine

Impulse stage

Reaction stage

Laval turbines and Pelton turbines show minimal the reaction. In for case working machines, low reactions are used in certain fans also. At low reaction, compressive force on the rotor is small, calling these stages pressureless or impulse stages. Conversely, stages with significant reaction yield greater compressive force, termed overpressure or reaction stages.

Axial stage

Flow separation

In axial stages, as reaction increases, blade camber decreases (required momentum change drops), reducing sensitivity to flow separation.

Equations for calculating velocity distribution at ideal flow in turbomachine

Ideal flow equations are derived for ideal fluid flow without internal losses. Although they are ideal flow equations, they are crucial for basic design of turbomachinery flow components, prediction of properties, analysis of the effect of flow component shape on internal losses of the machine, and understanding the causes of failures or problem operation of turbomachines.

The basic equations describing ideal flow velocities are the potential flow equations. The flow is considered to be potential (meaning that the velocity can only be calculated using the coordinates of a point according to a potential function V=f(x, y, z) in the case of a orthogonal coordinate system, or according to a function V=f(r, θ, a) in the case of a cylindrical coordinate system), where such a flow is referred to as an axisymmetric potential flow. Other quantities of ideal flow can be calculated from the energy equations and the Euler equation of hydrodynamics.

KeywordsChapter: Equations for calculating velocity distribution at ideal flow in turbomachine
2.9

Equation of axisymmetric potential flow

For potential flow, the curl velocity vector must be zero throughout the volume (Equation 8a). For axisymmetric flow, gradients of velocity components in the tangential direction (Equation 8b) must be zero in a cylindrical coordinate system, because the tangential coordinates are closed and the velocity at the origin of the tangential axis must be identical to that at the end of the coordinates. These conditions yield special velocity Equations (8c-h), applicable to other fluid quantities.

Axisymmetric potential flow conditions
8: Axisymmetric potential flow conditions
θ [°] azimuth in cylindrical coordinate system; C [m2·s-1] constant (e.g., proposed magnitude of product of tangential component of absolute velocity Vθ on mean radius). The modification of these equations is shown in Appendix 16.

Circulation of velocity

Euler work

The product r·Vθ is called the circulation of the tangential component of the velocity, which is constitutive, so it has the same properties as the irrotational vortex [Škorpík, 2023, p. 1.40]. If the circulation is constant, then the difference of the circulations in front of and behind the rotor is also constant and then also according to the Euler work equation (Equation 4) the Euler work of the potential flow will be constant along the length of the blades, see Problem 8.

Spiral casing

Bladeless stator

The equations of axisymmetric potential flow can also be applied to spiral paths, for example in spiral casings (Problem 9) or in bladeless stators (Problem 10).

Euler equation of hydrodynamics

Pressure gradinet

The Euler equation of hydrodynamics for potential flow can also be used to calculate other state variables, for example, the article Internal fluid friction and boundary layer development [Škorpík, 2023b]. From this equation one can read, among other things, that the pressure gradient of a potential flow without the effect of gravitational acceleration cannot have a tangential component, because the gradient of velocity respectively kinetic energy does not have one either, see Problem 8.

KeywordsChapter: Problems
2.10

Problems

Problem 1:
What force acts on the pipe between flanges due to fluid flow (see figure)? The inner pipe diameter is 23 mm, the flange height difference is 1,2 m, static pressure in the pipe versus outside pressure is 2 m water column, flow velocity is 4 m·s-1, and it's frictionless flow. Water is flowing in the pipe. You are considering frictionless flow. The solution of this problem is shown in Appendix 1.
d [m] pipe diameter; pat [Pa] atmospheric pressure; z [m] altitude coordinate.
1:   entry:   d; z; zH2O; V 4:   calculation:   Fh,x; A; m; p1; p2; Fp,x; Fx
2:   derivation:   eq. for Fx; Fy; Fz 5:   calculation:   VC; m; Fh,z; Fpz; Fz
3:   read off:   ρ; g; pat 6:   calculation:   Fy
Symbol descriptions are in Appendix 1.
Problem 2:
Determine the force and its components from the fluid flow acting on the radial fan blade. 88,8 kg·h-1 of air flows through the fan, the pressure p1 upstream of the impeller is atmospheric, the pressure difference between the impeller inlet and outlet is insignificant and the number of blades is 52. The other parameters are: r1=32,5 mm, r2=37,5 mm, V1=3,4 m·s-1, V2=9,34 m·s-1, α2=18,4°. The width of the impeller is 30 mm. The solution of this problem is shown in Appendix 2.
Low pressure radial fan velocity triangle
r [m] r [m] radius; α [°] angle of absolute velocity.
KeywordsChapter: Problems
2.11
1:   entry:   m; p1; z; r1; r2; V1; V2; α2; b 3:   calculation:   V2θ; Fθ
2:   calculation:   V2r; Fp,r; Fr 4:   calculation:   F
Symbol descriptions are in Appendix 2.
Problem 3:
Calculate force on a Kaplan turbine rotor blades from water flow and outlet pressure p2. Blade tips radius: 1850 mm, hub radius: 985 mm, tangential velocity: 15,3 m·s-1, axial velocity: 13 m·s-1, turbine rotational speed: 230,8 min-1. 56 m water column above turbine. Velocity triangle shapes at mean radius shown in attached figure. The solution of this problem is shown in Appendix 3.
A [m2] flow area. The index h indicates hub of the blade, the index m indicates the mean square radius of the blade, the index t indicates the tip of the blade.
1:   entry:   rt; rh; V1θ; Va; V2; N; z 4:   calculation:   rm; U; -W2θ; W1θ; Wmθ; Wm; βm; ε; Fa; F
2:   read off:   ρ 5:   read off:   pat; g
3:   calculation:   A1; A2; Q; m; Fθ   calculation:   V1; p1; p2
Symbol descriptions are in Appendix 3.
Problem 4:
Calculate the Euler work and Euler efficiency at the mean radius of the axial stage of the steam turbine and the internal work and efficiency of this stage. The stage has been designed by 1D calculation hence it has straight blades. The meridional velocity is constant (V0a=V2a). The isentropic gradient of the stage is 21,3 kJ·kg-1. The calculated total loss of the stage is 6 kJ·kg-1. The parameters of the velocity triangles at the mean radius are: V1=W2=148,68 m·s-1, V0=V2=W1=63,249 m·s-1, U1=U2=102,1 m·s-1. The solution of this problem is shown in Appendix 4.
KeywordsChapter: Problems
2.12
(a) cross-section of stage; (b) Euler work along length of blades; (c) energy balance of stage in h-s chart. h [J·kg-1] enthalpy; s [J·kg-1·K-1] entropy; wis [J·kg-1] internal work of the stage at isentropic expansion (expansion without losses);wE,is [J·kg-1] Euler work at flow without losses; Lw [J·kg-1] internal losses of the stage. The index s denotes the total state.
1:   entry:   Δhis; Lw; V1; W2; V0; V2; W1; U1; U2 3:   calculation:   wi
2:   calculation:   wE 4:   calculation:   wis; ηE; ηi
Symbol descriptions are in Appendix 4.
Problem 5:
Calculate the reaction of the axial stage of a steam turbine. If you know the velocity triangle. The solution of this problem is shown in Appendix 5.
Rychlostní trojúhleník parní turbíny v úloze
1:   entry:   V1; V2; W1; W2 3:   calculation:   wE; Δhs; R
2:   calculation:   ΔhR    
Symbol descriptions are in Appendix 5.
Problem 6:
Determine the reaction of a radial fan with forward curved blades if the stagnation pressure increase in the fan is 135 Pa, the working gas density is 1,2 kg·m-3, the blade speed at the outlet of the rotor is 10 m·s-1 and the blade speed at the inlet of the rotor is 8,7 m·s-1. The rotor blade passages are designed for equality of relative velocities (W1=W2). The solution of this problem is shown in Appendix 6.
Radial fan with forward curved blades
KeywordsChapter: Problems
2.13
1:   entry:   Δps; ρ; U2; U1 3:   calculation:   ΔhR; R
2:   calculation:   Δhs    
Symbol descriptions are in Appendix 6.
Problem 7:
Calculate the reaction of the Francis turbine at its mean radius. The radius of the impeller at the inlet is 1 m. The absolute velocity in front of the impeller is 35 m·s-1, behind the impeller is 12 m·s-1 (it has no tangential component). The turbine rotational speed is 375 min-1. The angle of absolute velocity is 20°. The height difference between the inlet and outlet of the impeller is 0,8 m. The density of water is 1000 kg·m-3. The solution of this problem is shown in Appendix 7.
Francisova turbína a její rychlostní trojúhelník
1:   entry:   r1; V1; V2; N; α1; Δz, ρ 4:   derivation:   equation for ΔpR
2:   derivation:   equation for Δps 5:   read off:   g; Lw,0-2; Lw,1-2
3:   calculation:   U1; V1θ; wE 6:   calculation:   R
Symbol descriptions are in Appendix 7.
Problem 8:
Calculate the parameters of the velocity triangle, pressure and reaction at the hub, mean square radius and tip of the Kaplan turbine blade. The required Euler work is 548 J·kg-1. The rotor dimensions, rotational speed, axial velocity at the mean square radius, and pressure behind the rotor are the same as in Problem 3. The absolute velocity at the rotor exit has only the axial direction. Also determine the pressure gradient in front of and behind the turbine rotor. Consider the potential flow of an ideal fluid. The solution of this problem is shown in Appendix 8.
Kaplan turbine state variables and velocity triangles
(a) pressure gradient in front of rotor; (b) changes in absolute and relative velocities at investigated radii; (c) effect of change in relative velocities on shape of blade passage, or blade twist; (d) distribution of tangential component of absolute velocity in front of rotor; (e) distribution of pressure in front of rotor; (f) distribution of reaction along blade length. β [°] angle of relative velocity.
KeywordsChapter: Problems
2.14
1:   entry:   wE; rt; rh; N; Va; V2; p2; ρ 6:   calculation:   p1h; p1m; p1t
2:   calculation:   rm; Uh; Um; Ut; V1θh; V1θm; V1θt 7:   calculation:   Δps; ΔpRh; ΔpRm; ΔpRt; Rh; Rm; Rt
3:   calculation:   V1h; V1m; V1t; α1h; α1m; α1t 8:   derivation:   equation for grad p1
4:   calculation:   W1θh; W1θm; W1θt; W1h; W1m; W1t; β1h; β1m; β1t 9:   derivation:   equation for Δp1
5:   calculation:   W2h; W2m; W2t; β2h; β2m; β2t    
Symbol descriptions are in Appendix 8.
Problem 9:
The purpose of the spiral casings of radial machines is to discharge or feed the working fluid from/to the blade section. The flow in such a casing has a spiral path. The figure shows a section of a radial fan with backward curved blades and a spiral casing - suggest the dimensions of this spiral casing if there is a bladeless diffuser between it and the rotor. Determine the pressure at the outlet of the bladeless diffuser (between radii r2 and r3). Prove that when an incompressible fluid flows through a radial duct of constant width b, the spiral path is a logarithmic spiral. Discuss the effect of internal friction in the fluid on the shape of the spiral path. What is the velocity and pressure distribution at the exit of the spiral casing? Consider incompressible potential flow. Discuss the effect of the casing width on the radius of the casing. The parameters of the fan are R=0,65; r3=215 mm; r2=170 mm; r1=118,5 mm; b2=101,5 mm; b1=120 mm; N=1360 min-1. The increase in stagnation pressure in the fan is 500 Pa. The air flow through the fan is 1200 m3·h-1 and its stagnation suction pressure is atmospheric at a density of 1,2 kg·m-3. The solution of the problem and other conclusions are shown in Appendix 9.
Spiral casing
(a) velocity triangles; (b) velocity profile at outlet of spiral casing; (c) pressure profile at outlet of spiral casing. Ψ-spiral absolute velocity trajectory.
KeywordsChapter: Problems
2.15
1:   entry:   R; r3; r2; r1; b2; b1; Δps; N; Q; p1s; ρ 5:   calculation:   p3s; V3θ; V3r; V3; p3
2:   derivation:   equation for rθ 6:   proof:   α=const.
3:   calculation:   wE; U2; V2θ; C 7:   discussion:   on effect of friction
4:   calculation:   rθ for selected θ 8:   discussion:   velocity and pressure distribution at casing outlet
Symbol descriptions are in Appendix 9.
Problem 10:
Design the outlet radius of the bladeless stator of a radial compressor, which is drawn in the figure. The stage parameters are: V2θ=300 m·s-1, V2r=90 m·s-1, r2=33 mm, p2=200 kPa, t2=82,9 °C. The stator pressure rise is 80 kPa. The working gas is air. Find also whether the angle between the absolute velocity in the bladeless stator and its tangential component (between radii r2 and r3) changes. Consider the compressible potential flow. The solution of this problem is shown in Appendix 10.
Flow behind radial stage rotor in bladeless diffuser
(a) rotor-bladeless stator assembly and inlet and outlet casing; (b) bladeless stator section; (c) absolute velocity at the inlet and outlet of the bladeless stator.
1:   entry:   V2θ; V2r; r2; p2; ΔpS; t2 4:   solution:   r3 z m2=m3
2:   read off:   h3; t3 from h-s chart 5:   calculation:   α2; α3
3:   calculation:   V3; ρ3 6:   comapare:   α2 vs α3
Symbol descriptions are in Appendix 10.

References

ŠKORPÍK, Jiří, 2024, Technická termomechanika, engineering-sciences.education, Brno, engineering-sciences.education/technicka-termomechanika.html.
ŠKORPÍK, Jiří, 2023, Technická matematika, engineering-sciences.education, Brno, engineering-sciences.education/technicka-matematika.html.
ŠKORPÍK, Jiří, 2023b, Vnitřní tření tekutiny a vývoj mezní vrstvy, fluid-dynamics.education, Brno, fluid-dynamics.education/vnitrni-treni-tekutiny-a-vyvoj-mezni-vrstvy.html.
ŠKORPÍK, Jiří, 2023c, Flow of gases and steam through nozzles, fluid-dynamics.education, Brno, fluid-dynamics.education/flow-of-gases-and-steam-through-nozzles.html.
ŠKORPÍK, Jiří, 2023d, Flow of gases and steam through diffusers, fluid-dynamics.education, Brno, fluid-dynamics.education/flow-of-gases-and-steam-through-diffusers.html.
©Jiří Škorpík, LICENCE